Question

10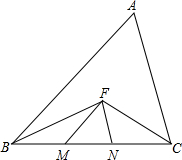．已知，如图∠ABC、∠ACB的平分线相交于点F，过F作FM∥AB交BC于点M，过F作FN∥AC交BC于点N，试说明△FMN的周长等于BC的长．

Answer 1

分析 根据DE∥BC，FM∥AB，FN∥AC，可证明四边形BDFM和四边形CEFN是平行四边形，再转化得出△FMN的周长等于BC．

解答 解：∵DE∥BC，FM∥AB，FN∥AC
∴四边形BDFM和四边形CEFN是平行四边形，
∴FM=BD，FN=CE，DF=BM，EF=CN，
∵BD=DF，CE=EF，
∴C_△FMN=FM+FN+MN=BM+CN+MN=BC．

点评 此题考查了平行线及角平分线的性质，等腰三角形的判定定理，熟练掌握等腰三角形的判定和性质是解题的关键．