题目内容
19.解不等式:|x-5|-|2x+3|<1.分析 根据绝对值的意义,分类讨论:当x≤-$\frac{3}{2}$时,不等式化为-x+5+2x+3<1;当-$\frac{3}{2}$<x≤5时,不等式化为-x+5-(2x+3)<1;当x>5时,不等式化为x-5-(2x+3)<1,然后分别解不等式确定每种情况下的x的范围,再把综合三种情况即可得到原不等式的解集.
解答 解:当x≤-$\frac{3}{2}$时,不等式化为-x+5+2x+3<1,解得x<-7;
当-$\frac{3}{2}$<x≤5时,不等式化为-x+5-(2x+3)<1,解得x>1,所以1<x≤5;
当x>5时,不等式化为x-5-(2x+3)<1,解得x<-9,所以x>5,
所以原不等式得解为x<-7或x>1.
点评 本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.确定x的取值范围去绝对值是解决此题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
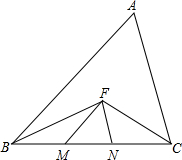 已知,如图∠ABC、∠ACB的平分线相交于点F,过F作FM∥AB交BC于点M,过F作FN∥AC交BC于点N,试说明△FMN的周长等于BC的长.
已知,如图∠ABC、∠ACB的平分线相交于点F,过F作FM∥AB交BC于点M,过F作FN∥AC交BC于点N,试说明△FMN的周长等于BC的长. 如图所示,在直角坐标系xOy中,已知一次函数y=-$\frac{1}{2}$x+2的图象于x轴,y轴分别交于A,D两点,四边形ABCD是正方形
如图所示,在直角坐标系xOy中,已知一次函数y=-$\frac{1}{2}$x+2的图象于x轴,y轴分别交于A,D两点,四边形ABCD是正方形 已知△ABC三个内角的平分线相交于点O,OG⊥AB,垂足为G,∠1=∠AOE,∠2=∠BOG,证明:∠1=∠2.
已知△ABC三个内角的平分线相交于点O,OG⊥AB,垂足为G,∠1=∠AOE,∠2=∠BOG,证明:∠1=∠2.