题目内容
1.已知△ABC∽△A′B′C′,且$\frac{AB}{A′B′}$=2,AD⊥BC于点D,A′D′⊥B′C′于点D′,点P,P′分别在BC和B′C′上,BP=$\frac{1}{3}$BC,B′P′=$\frac{1}{3}$B′C′,则$\frac{{S}_{△ADP}}{{S}_{△A}{′}_{D}{′}_{P}′}$=4.分析 根据相似三角形的性质得到$\frac{AB}{A′B′}$=$\frac{AD}{A′D′}$=$\frac{BC}{B′C′}$=2,∠B=∠B′,利用$\frac{BP}{B′P′}$=$\frac{BC}{B′C′}$得到$\frac{AB}{A′B′}$=$\frac{BP}{B′P′}$,则可判断△ABP∽△A′B′P′,得到$\frac{AB}{A′B′}$=$\frac{AP}{A′P′}$,所以$\frac{AP}{A′P′}$=$\frac{AD}{A′D′}$,于是可判断Rt△ADP∽Rt△A′D′P′,然后根据相似三角形的性质易得$\frac{{S}_{△ADP}}{{S}_{△A}{′}_{D}{′}_{P}′}$=4.
解答 解:∵△ABC∽△A′B′C′,AD⊥BC于点D,A′D′⊥B′C′于点D′,
∴$\frac{AB}{A′B′}$=$\frac{AD}{A′D′}$=$\frac{BC}{B′C′}$=2,∠B=∠B′,
∵BP=$\frac{1}{3}$BC,B′P′=$\frac{1}{3}$B′C′,
∴$\frac{BP}{B′P′}$=$\frac{BC}{B′C′}$,
∴$\frac{AB}{A′B′}$=$\frac{BP}{B′P′}$,
而∠B=∠B′,
∴△ABP∽△A′B′P′
∴$\frac{AB}{A′B′}$=$\frac{AP}{A′P′}$,
∴$\frac{AP}{A′P′}$=$\frac{AD}{A′D′}$,
∴Rt△ADP∽Rt△A′D′P′,
∴$\frac{{S}_{△ADP}}{{S}_{△A}{′}_{D}{′}_{P}′}$=($\frac{AD}{A′D′}$)2=4.
故答案为4.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形(多边形)的周长的比等于相似比;相似三角形的面积的比等于相似比的平方.也考查了相似三角形的判定.

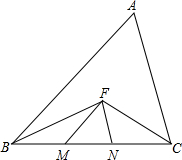 已知,如图∠ABC、∠ACB的平分线相交于点F,过F作FM∥AB交BC于点M,过F作FN∥AC交BC于点N,试说明△FMN的周长等于BC的长.
已知,如图∠ABC、∠ACB的平分线相交于点F,过F作FM∥AB交BC于点M,过F作FN∥AC交BC于点N,试说明△FMN的周长等于BC的长. 如图所示,在直角坐标系xOy中,已知一次函数y=-$\frac{1}{2}$x+2的图象于x轴,y轴分别交于A,D两点,四边形ABCD是正方形
如图所示,在直角坐标系xOy中,已知一次函数y=-$\frac{1}{2}$x+2的图象于x轴,y轴分别交于A,D两点,四边形ABCD是正方形