题目内容
把下列各式分解因式:
(1)3ax+6ay;
(2)4x3-9x;
(3)ax2+2a2x+a3;
(4)(x-2)2+x-8;
(5)(a2+ab+b2)2-9a2b2;
(6)(x2-x)(x2-x-8)+12;
(7)(a2-4ab+4b2)-(2a-4b)+1;
(8)b2+c2-2bc-a2.
(1)3ax+6ay;
(2)4x3-9x;
(3)ax2+2a2x+a3;
(4)(x-2)2+x-8;
(5)(a2+ab+b2)2-9a2b2;
(6)(x2-x)(x2-x-8)+12;
(7)(a2-4ab+4b2)-(2a-4b)+1;
(8)b2+c2-2bc-a2.
考点:提公因式法与公式法的综合运用
专题:
分析:(1)直接提取公因式进而分解因式即可;
(2)首先提取公因式x,进而利用平方差公式分解因式即可;
(3)首先提取公因式x,进而利用完全平方公式分解因式即可;
(4)首先去括号,进而利用十字相乘法分解因式得出即可;
(5)直接利用平方差公式分解因式,进而利用完全平方公式分解因式即可;
(6)利用十字相乘法分解因式得出即可;
(7)利用完全平方公式分解因式得出即可;
(8)利用完全平方公式以及平方差公式分解因式得出即可.
(2)首先提取公因式x,进而利用平方差公式分解因式即可;
(3)首先提取公因式x,进而利用完全平方公式分解因式即可;
(4)首先去括号,进而利用十字相乘法分解因式得出即可;
(5)直接利用平方差公式分解因式,进而利用完全平方公式分解因式即可;
(6)利用十字相乘法分解因式得出即可;
(7)利用完全平方公式分解因式得出即可;
(8)利用完全平方公式以及平方差公式分解因式得出即可.
解答:解:(1)3ax+6ay=3a(x+2y);
(2)4x3-9x=x(4x2-9)=x(2x+3)(2x-3);
(3)ax2+2a2x+a3=a(x+a)2;
(4)(x-2)2+x-8
=x2-4x+4+x-8
=x2-3x-4
=(x-4)(x+3);
(5)(a2+ab+b2)2-9a2b2
=(a2+ab+b2+3ab)(a2+ab+b2-3ab)
=(a2+4ab+b2)(a-b)2;
(6)(x2-x)(x2-x-8)+12
=(x2-x)2-8(x2-x)+12
=(x2-x-6)(x2-x-2)
=(x-3)(x+2)(x-2)(x+1);
(7)(a2-4ab+4b2)-(2a-4b)+1
=(a-2b)2-2(a-2b)+1
=(a-2b-1)2;
(8)b2+c2-2bc-a2
=(b-c)2-a2
=(b-c+a)(b-c-a).
(2)4x3-9x=x(4x2-9)=x(2x+3)(2x-3);
(3)ax2+2a2x+a3=a(x+a)2;
(4)(x-2)2+x-8
=x2-4x+4+x-8
=x2-3x-4
=(x-4)(x+3);
(5)(a2+ab+b2)2-9a2b2
=(a2+ab+b2+3ab)(a2+ab+b2-3ab)
=(a2+4ab+b2)(a-b)2;
(6)(x2-x)(x2-x-8)+12
=(x2-x)2-8(x2-x)+12
=(x2-x-6)(x2-x-2)
=(x-3)(x+2)(x-2)(x+1);
(7)(a2-4ab+4b2)-(2a-4b)+1
=(a-2b)2-2(a-2b)+1
=(a-2b-1)2;
(8)b2+c2-2bc-a2
=(b-c)2-a2
=(b-c+a)(b-c-a).
点评:此题主要考查了公式法分解因式以及提取公因式法和十字相乘法分解因式,熟练应用十字相乘法分解因式是解题关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
十年后,909班学生聚会,见面时相互间均握了一次手,好事者统计:一共握了780次.你认为这次聚会的同学有( )人.
| A、38 | B、39 | C、40 | D、41 |
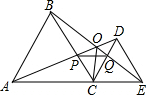 如图,C为AE上一点,在AE同侧分别作等边△ABC和等边△CDE,AD与BC交于点P,BE与CD交于Q,连接PQ.求证:∠AOB=60°.
如图,C为AE上一点,在AE同侧分别作等边△ABC和等边△CDE,AD与BC交于点P,BE与CD交于Q,连接PQ.求证:∠AOB=60°.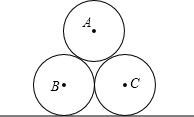 如图,某城市公园的雕塑是焊接固定在水平地面上的3个直径均为2m的两两外切的圆,请求出雕塑的最高点到地面的距离.(提示:构建适当的三角形辅助解答)
如图,某城市公园的雕塑是焊接固定在水平地面上的3个直径均为2m的两两外切的圆,请求出雕塑的最高点到地面的距离.(提示:构建适当的三角形辅助解答) 操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a、b、c(如图①),分别用4张这样的直角三角形纸片拼成如图②③的形状,图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系?你能得到a、b、c之间有什么关系?
操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a、b、c(如图①),分别用4张这样的直角三角形纸片拼成如图②③的形状,图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系?你能得到a、b、c之间有什么关系? 用一张扇形的纸片卷成一个如图所示的圆锥模型,要求圆锥的母线长为6cm,底面圆的直径为8cm,那么这张扇形纸片的面积是
用一张扇形的纸片卷成一个如图所示的圆锥模型,要求圆锥的母线长为6cm,底面圆的直径为8cm,那么这张扇形纸片的面积是