题目内容
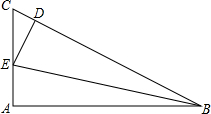在直角△ABC中，∠A=90°，∠ABC的平分线BE交AC于E点，过E点作ED⊥BC于D点，已知AC=10cm，△CDE的周长为16cm，求：CD的长．考点：角平分线的性质,勾股定理
专题：
分析：根据角平分线上的点到角的两边的距离相等可得AE=DE，从而求出DE+CE=AC，所以△CDE的周长=AC+CD，根据△CDE的周长为16cm即可求得CD的长．
解答：解：∵BE为∠ABC的角平分线，∠A=90°，DE⊥BC，
∴AE=DE，
∴DE+CE=AE+CE=AC=10cm，
∵△CDE的周长为16cm，
∴DE+CE+CD=16cm，
∴CD=16-10=6cm．
∴AE=DE，
∴DE+CE=AE+CE=AC=10cm，
∵△CDE的周长为16cm，
∴DE+CE+CD=16cm，
∴CD=16-10=6cm．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质并推出△CDE的周长等于AC+CD是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，点D、E分别在BC、AC上，BE平分∠ABC，DE∥BA，如果CE=10，AE=6，△CDE的周长为34，求DE的长．
如图，△ABC中，AB=AC，AD∥CB，求证：AD平分∠CAE．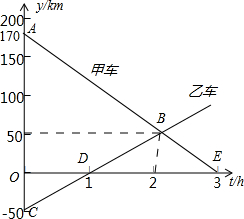
甲、乙两辆汽车在同一条公路上同时匀速行驶，图中的两条线分别表示甲、乙两车距M站的距离y（km）与它们行驶的时间t（h）之间的函数关系式，请根据图象回答下列问题．