题目内容
10.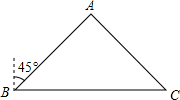 某物流公司派送人员甲、乙分别从B地派送货物到A、C两地,如图,A在B的北偏东45°方向,C在B的正东方向且BC=120km.乙的速度是60km/h,甲的速度是乙速度的$\sqrt{2}$倍,甲把货物送到A地后又接到A地一批货物要送到C地,结果两人同时到达C地.
某物流公司派送人员甲、乙分别从B地派送货物到A、C两地,如图,A在B的北偏东45°方向,C在B的正东方向且BC=120km.乙的速度是60km/h,甲的速度是乙速度的$\sqrt{2}$倍,甲把货物送到A地后又接到A地一批货物要送到C地,结果两人同时到达C地.(1)∠BAC=90°;
(2)若甲乙两人间的距离为s,请写出s(km)与乙出发时间t(h)的函数表达式;并写出当t为何值时,两人间的距离最大?(注:货物交接时间忽略不计)
分析 (1)作AD⊥BC于D,由题意求出∠ABC=45°,△ABD是等腰直角三角形,得出AB=$\sqrt{2}$BD,由甲的速度是乙速度的$\sqrt{2}$倍,得出△ACD是等腰直角三角形,∠DAC=45°,求出∠BAC=90即可;
(2)由(1)得出△ABC是等腰直角三角形,AD=BD=CD,由乙的速度求出乙到C地的时间,得出当0<t≤1时,s=60t;当1<t≤2时,s=120-60t;即可得出结论.
解答 解:(1)作AD⊥BC于D,如图所示: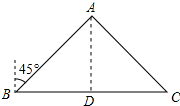
由题意得:∠ABC=90°-45°=45°,
∴△ABD是等腰直角三角形,
∴AB=$\sqrt{2}$BD,
∵甲的速度是乙速度的$\sqrt{2}$倍,
∴AC=$\sqrt{2}$CD,
∴△ACD是等腰直角三角形,
∴∠DAC=45°,
∴∠BAC=45°+45°=90°;
故答案为:90;
(2)由(1)得:△ABC是等腰直角三角形,AD=BD=CD,
∵乙的速度是60km/h,BC=120km,
∴120÷60=2(h),
∴当0<t≤1时,s=60t;
当1<t≤2时,s=120-60t;
当t=1时,s=AD=$\frac{1}{2}$BC=60,
即当t为何值时,两人间的距离最大,最大值是60km.
点评 本题考查了解直角三角形的运用-方向角问题、等腰直角三角形的判定与性质;证出∠BAC=90°是解决问题的关键.

练习册系列答案
相关题目
1.“双十一”购物节后,小明对班上同学中的12位进行抽样调查并用数字1-12对每位被调查者进行编号,统计每位同学在购物节中的消费金额,结果如表所示:
根据上表统计结果,被调查的同学在“双十一”购物节中消费金额的平均数和众数分别为( )
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 消费金额(元) | 300 | 200 | 400 | 500 | 400 | 300 | 600 | 300 | 400 | 800 | 300 | 300 |
| A. | 400,300 | B. | 300,400 | C. | 400,400 | D. | 300,300 |
5.某舞蹈队10名队员的年龄分布如表所示:
则这10名队员年龄的众数是14岁.
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数 | 2 | 4 | 3 | 1 |
15.在一个不透明的布袋中装有3个白球和5个红球,它们除了颜色不同外,其余均相同,从中随机摸出一个球,摸到红球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{8}$ |
20.与-2的乘积为1的数是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
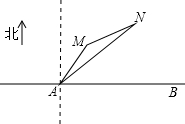 如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).
如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4). 光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其它天气平均每天可发电5度,已知某月(按30天计)共发电550度.
光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其它天气平均每天可发电5度,已知某月(按30天计)共发电550度.