题目内容
3.在一场篮球比赛中,有位明星球员得61分,在这61分中有3分球,也有2分球(没有罚球).请你思考一下这名球员在61分中3分球的概率最大是多少?最小概率是多少?分析 首先设2分球x个,3分球y个,则2x+3y=61,进而利用二元一次方程的解进行分析,再根据概率公式得出即可.
解答 解:设2分球x个,3分球y个,则2x+3y=61,
当x=1,y=$\frac{59}{3}$不合题意舍去;
当x=2,y=19;
…
当x=28,y=$\frac{5}{3}$,不合题意;
当x=29,y=1.
故这名球员在61分中3分球的概率最大是$\frac{19}{2+19}$=$\frac{19}{21}$,最小概率是$\frac{1}{29+1}$=$\frac{1}{30}$.
点评 此题主要考查了概率公式、二元一次方程的应用,利用总分为61分得出正确等量关系进而求出是解题关键.

练习册系列答案
相关题目
14.下列计算正确的是( )
| A. | a2+a3=2a5 | B. | a2•a3=a6 | C. | (a2)3=a8 | D. | a4÷a3=a |
8.表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )
| 甲方案 | 乙方案 | |
| 门号的月租费(元) | 400 | 600 |
| MAT手机价格(元) | 15000 | 13000 |
| 注意事项:以上方案两年内不可变更月租费 | ||
| A. | 500 | B. | 516 | C. | 517 | D. | 600 |
15.在一个不透明的布袋中装有3个白球和5个红球,它们除了颜色不同外,其余均相同,从中随机摸出一个球,摸到红球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{8}$ |
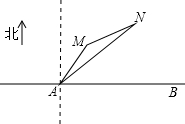 如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).
如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).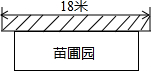 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.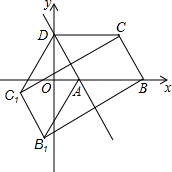 如图,已知?ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D
如图,已知?ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D