题目内容
6.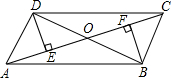 已知:如图,在四边形ABCD中,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF,∠ADB=∠CBD.
已知:如图,在四边形ABCD中,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF,∠ADB=∠CBD.求证:四边形ABCD是平行四边形.
分析 首先利用平行线的性质与判定方法得出∠DAE=∠BCF,进而利用AAS得出△ADE≌△CBF,即可得出AD$\stackrel{∥}{=}$BC,即可得出答案.
解答 证明:∵∠ADB=∠CBD,
∴AD∥BC,
∴∠DAE=∠BCF,
在△ADE和△CBF中
∵$\left\{\begin{array}{l}{∠DAE=∠BCF}\\{∠AED=∠CFB}\\{DE=BF}\end{array}\right.$,
∴△ADE≌△CBF(AAS),
∴AD=BC,
∴四边形ABCD是平行四边形.
点评 此题主要考查了全等三角形的判定与性质以及平行四边形的判定,正确得出△ADE≌△CBF(AAS)是解题关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
14.下列说法:
①两条线段的比是两条线段的长度比,比值是个正数;
②两条线段的长度比是“同一单位下”的长度比;
③两条线段的比与所采用的单位无关;
④两条线段的比有顺序,$\frac{a}{b}$与$\frac{b}{a}$不同,它们互为倒数.
其中正确的说法有( )
①两条线段的比是两条线段的长度比,比值是个正数;
②两条线段的长度比是“同一单位下”的长度比;
③两条线段的比与所采用的单位无关;
④两条线段的比有顺序,$\frac{a}{b}$与$\frac{b}{a}$不同,它们互为倒数.
其中正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.下列说法错误的是( )
| A. | 符号相反的两个数互为相反数 | |
| B. | 一个正数的绝对值越大,在数轴上表示它的点就越靠右 | |
| C. | 一个数的绝对值越大,在数轴上表示它的点离原点就越远 | |
| D. | 当a≠0时,|a|总是大于0 |
18.某文具店在一周的销售中,盈亏情况如下表(盈余为正,单位:元)
表中星期四的盈亏被墨水涂污了,请你算出星期四的盈亏数,并说明星期四是盈还是亏?盈亏是多少?
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
| -27.8 | -60.8 | 200 |  | -8 | 128.1 | 168 | 481 |
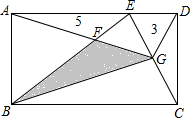 如图,长方形ABCD中,C、G、E在同一条直线上,并且其中有两块小三角形的面积已经标出,求阴影部分的面积.
如图,长方形ABCD中,C、G、E在同一条直线上,并且其中有两块小三角形的面积已经标出,求阴影部分的面积.