若关于x的方程$\frac{x+4}{x-3}$=$\frac{m}{x-3}$+2有增根.则m的值是( )A．7B．3C．4D．0 题目和参考答案——青夏教育精英家教网—

题目内容

13．若关于x的方程$\frac{x+4}{x-3}$=$\frac{m}{x-3}$+2有增根，则m的值是（　　）

A．

B．

C．

D．

分析分式方程去分母转化为整式方程，由分式方程有增根，得到x-3=0，求出x的值，代入整式方程求出m的值即可．

解答解：分式方程去分母得：x+4=m+2x-6，
由分式方程有增根，得到x-3=0，即x=3，
把x=3代入整式方程得：m=7，
故选A

点评此题考查了分式方程的增根，增根问题可按如下步骤进行：①让最简公分母为0确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．

练习册系列答案

相关题目

	A．	一个三角形中至少有一个角不少于60°
	B．	三角形的中线不可能在三角形的外部
	C．	周长相等的两个三角形全等
	D．	三角形的中线把三角形的面积平均分成相等的两部分

4．

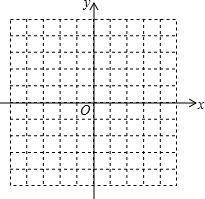已知在等腰△ABC中，AB=AC，对称轴为x轴，点A的坐标为（-3，0），点B的坐标为（1，3）．
（1）请画出△ABC；
（2）如果△ABC关于y轴对称的三角形为△A₁B₁C₁，请写出△A₁B₁C₁三个顶点的坐标：
点A的对称点A₁的坐标是（3，0），点B的对称点B₁的坐标是（-1，3），点C的对称点C₁的坐标是（-1，-3）；
（3）如果点D的坐标为（5，-3），将△ABC左右平移，使点C与点D重合，那么点A平移的方向是向右，距离是4个单位．

1．

如图，在平行四边形ABCD中，AB=3，BC=5，对角线AC、BD相交于点O，则OA的取值范围是（　　）

8．直线y=kx+b-1不经过第二象限，则k，b的情况是（　　）

18．（1）计算：[-2⁴×（3-2×2⁰）÷（-2）^-2÷2⁶]×4÷10^-2
（2）先化简，后求值：（1-$\frac{2}{x+1}$）²÷$\frac{x-1}{x+1}$，其中x=$\frac{1}{3}$
（3）解方程：$\frac{2}{2-x}$+$\frac{{x}^{2}}{{x}^{2}-4}$+$\frac{1}{x+2}$=1．

5．

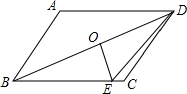如图，在?ABCD中，O是对角线BD的中点，且AB≠AD，过点O作OE⊥BD于点E，若?ABCD的周长为20，则△CDE的周长为10．

2．

如图，将△ABC沿BC方向平移至△DEF的位置，若BC=5，BF=15
（1）△ABC向右平移的距离AD=10
（2）已知△ABC的周长为18，则四边形ABFD的周长等于38．

3．某学校把学生的期末测试、实践能力两项成绩分别按60%，40%的比例计入学期总成绩，小明实践能力的得分是80分，期末测试的得分是90分，则小明的学期总成绩是（　　）

试题分类