题目内容
9.已知关于x的方程(m2-2m-3)x2-(m+5)x-2=0有正整数根,求m的值.分析 ①当m2-2m-3≠0时,方程有两个正整数根,说明根的判别式△=b2-4ac≥0,即(m+5)2-4×(m2-2m-3)×(-2)≥0,由此可以求出m的取值范围,然后根据方程有两个正整数根确定m的值,②当m2-2m-3=0时,然后根据方程有两个正整数根确定m的值.
解答 解:∵关于x的方程(m2-2m-3)x2-(m+5)x-2=0有正整数根,
①当m2-2m-3≠0时,
∴△=b2-4ac≥0,即(m+5)2-4×(m2-2m-3)×(-2)≥0,
∴(3m-1)2≥0,
∴m取任意实数,方程(m2-2m-3)x2-(m+5)x-2=0有实数根,
解方程(m2-2m-3)x2-(m+5)x-2=0得:x1=$\frac{2}{m-3}$,x2=-$\frac{1}{m+1}$,
∴x1=$\frac{2}{m-3}$>0,x2=-$\frac{1}{m+1}$>0,
∴m=-2或4或5,
∴当m的值是-2或4或5,使关于x的方程(m2-2m-3)x2-(m+5)x-2=0有正整数根,
②当m2-2m-3=0时,即(m+5)x+2=0有正整数根,
∴m=-3,m=1,
当m=-3,m=1时,2x+2=0或6x+2=0,
解得:x=-1,或x=-$\frac{1}{3}$,均不符合题意,
∴不存在m的值,使关于x的方程(m2-2m-3)x2-(m+5)x-2=0有正整数根.
点评 本题考查的是根的判别式,根据题意利用根与系数的关系以及根的判别式得出是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.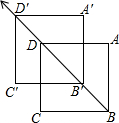 如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
 如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )
如图,先将正方形ABCD沿BD方向平移,平移的距离为线段BD长的一半,得到像A′B′C′D′,我们发现原图形和像组成的图中有3个正方形,再将正方形A′B′C′D′作类似的第二次、第三次…平移变换.如果经过12次平移变换,那么原图形和所有像组成的图形中有多少个正方形?( )| A. | 25 | B. | 39 | C. | 47 | D. | 49 |
17.下列合并同类项,结果正确的是( )
| A. | x4+x4=x8 | B. | 5m-2m+4m=7m | ||
| C. | 15a+4a-11=18a | D. | -9xy-2xy+11xy=xy |
4.已知一弹簧称所挂重物质量x(g)与弹簧长度y(cm)之间的关系如下表:
(1)请写出弹簧长度y(cm)与所挂物体重量x(g)之间的关系式.
(2)当所挂重物质量为4.5g时,弹簧长度是多少厘米?
| x(g) | 2 | 3 | 4 | 5 | 6 | 7 | … |
| y(cm) | 8.2 | 8.3 | 8.4 | 8.5 | 8.6 | 8.7 | … |
(2)当所挂重物质量为4.5g时,弹簧长度是多少厘米?
 已知:如图,在平行四边形ABCD中,点M,N在对角线AC上,且AM=CN.求证:四边形BMDN是平行四边形.
已知:如图,在平行四边形ABCD中,点M,N在对角线AC上,且AM=CN.求证:四边形BMDN是平行四边形. 如图所示,M是梯形ABCD的腰CD的中点,MN⊥AB,垂足为N.求证:S△ABM=$\frac{1}{2}$梯形ABCD.
如图所示,M是梯形ABCD的腰CD的中点,MN⊥AB,垂足为N.求证:S△ABM=$\frac{1}{2}$梯形ABCD.