题目内容
9.解不等式:(1)3(x-1)>2x+2;
(2)$\frac{3x+1}{3}-\frac{7x-3}{5}≤2+\frac{2(x-2)}{15}$.
分析 (1)去括号,移项,合并同类项,系数化成1即可;
(2)去分母,去括号,移项,合并同类项,系数化成1即可.
解答 解:(1)3(x-1)>2x+2,
3x-3>2x+2,
3x-2x>2+3,
x>5;
(2)去分母得:5(3x+1)-3(7x-3)≤30+2(x-2),
15x+5-21x+9≤30+2x-4,
15x-21x-2x≤30-4-5-9,
-8x≤12,
x≥-$\frac{3}{2}$.
点评 本题考查了解一元一次不等式的应用,能根据不等式的基本性质正确解不等式是解此题的关键,注意:解一元一次不等式的步骤是:去分母,去括号,移项,合并同类项,系数化成1.

练习册系列答案
相关题目
20.下列事件中,是确定事件的是( )
| A. | 度量三角形的内角和,结果是360° | B. | 射击运动员射击一次,命中9环 | ||
| C. | 明天会下雨 | D. | 买一张电影票,座位号是奇数 |
14.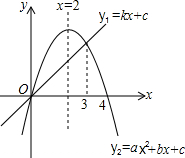 一次函数y1=kx+c与二次函数y2=ax2+bx+c的图象如图所示,则下列结论中:①k<0;②a>0;③c=0;④方程ax2+bc+c=0的两个根为0或4;⑤当y1≥y2时,x的取值范围是x≤0若x≥3.其中正确的个数有( )
一次函数y1=kx+c与二次函数y2=ax2+bx+c的图象如图所示,则下列结论中:①k<0;②a>0;③c=0;④方程ax2+bc+c=0的两个根为0或4;⑤当y1≥y2时,x的取值范围是x≤0若x≥3.其中正确的个数有( )
 一次函数y1=kx+c与二次函数y2=ax2+bx+c的图象如图所示,则下列结论中:①k<0;②a>0;③c=0;④方程ax2+bc+c=0的两个根为0或4;⑤当y1≥y2时,x的取值范围是x≤0若x≥3.其中正确的个数有( )
一次函数y1=kx+c与二次函数y2=ax2+bx+c的图象如图所示,则下列结论中:①k<0;②a>0;③c=0;④方程ax2+bc+c=0的两个根为0或4;⑤当y1≥y2时,x的取值范围是x≤0若x≥3.其中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列各式为最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\frac{\sqrt{15}}{2}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\frac{\sqrt{12}}{5}$ |
 已知二次函数y=ax2+bx+c的图象过点(1,0),(-3,0),(0,$\frac{3}{2}$).
已知二次函数y=ax2+bx+c的图象过点(1,0),(-3,0),(0,$\frac{3}{2}$).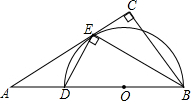 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.