题目内容
1.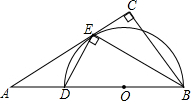 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.(1)判断直线AC与△DBE外接圆的位置关系,并说明理由;
(2)若AD=4,AE=4$\sqrt{2}$,求BC的长.
分析 (1)先证明BD为△DBE外接圆的直径,连接OE,再证出∠OEB=∠CBE,由∠CBE+∠CEB=90°,得出∠OEB+∠CEB=90°,即AC⊥OE,即可得出结论;
(2)设OD=OE=OB=x,则OA=x+4,根据勾股定理得出方程,求出半径,得出AB=8,再证明△AOE∽△ABC,得出比例式$\frac{AO}{AB}=\frac{OE}{BC}$,即可求出BC的长.
解答 解:(1)直线AC与△DBE的外接圆相切;理由如下:
∵DE⊥BE,
∴∠BED=90°,
∴BD为△DBE外接圆的直径,
取BD的中点O(即△DBE外接圆的圆心),连接OE,如图所示: ∵OE=OB,
∵OE=OB,
∴∠OEB=∠OBE,
∵BE平分∠ABC,
∴∠OBE=∠CBE,
∴∠OEB=∠CBE,
∵∠CBE+∠CEB=90°,
∴∠OEB+∠CEB=90°,
即AC⊥OE,
∴直线AC与△DBE的外接圆相切;
(2)设OD=OE=OB=x,则OA=x+4,
∵AC⊥OE,
∴∠AEO=90°,
根据勾股定理得:OE2+AE2=OA2,
即x2+(4$\sqrt{2}$)2=(x+4)2,
解得:x=2,
∴OD=OB=2,
∴AB=AD+OD+OB=8,
∵∠A=∠A,∠AEO=∠ACB=90°,
∴△AOE∽△ABC,
∴$\frac{AO}{AB}=\frac{OE}{BC}$,
即$\frac{6}{8}=\frac{2}{BC}$,
∴BC=$\frac{8}{3}$.
点评 本题考查了切线的判定、圆周角定理、勾股定理、相似三角形的判定与性质;本题有一定难度,特别是(2)中,需要根据勾股定理列出方程和证明三角形相似才能得出结果.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
12.为了丰富学生课余活动,学校开展歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
则入围同学决赛的中位数和众数分别是( )
| 成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
| 人数 | 2 | 3 | 5 | 4 | 3 | 1 |
| A. | 9.60,9.60 | B. | 9.60,9.70 | C. | 9.70,9.60 | D. | 9.65,9.60 |
6.在函数y=$\frac{{\sqrt{x+3}}}{x-1}$中,自变量x的取值范围是( )
| A. | x≥-3且x≠1 | B. | x>-3且x≠1 | C. | x≥3 | D. | x>3 |
13.下列运算正确的是( )
| A. | (-a2)3=a6 | B. | (a+b)2=a2+b2 | C. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | D. | 5$\sqrt{5}$-$\sqrt{5}$=4 |
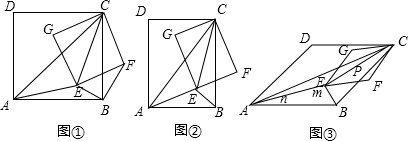
 在平行四边形ABCD中,O是对角线AC的中点,过点O作AC的垂线与AD、BC分别交于点E、F.
在平行四边形ABCD中,O是对角线AC的中点,过点O作AC的垂线与AD、BC分别交于点E、F.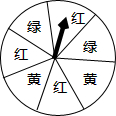 如图,一个转盘被分成7个相同的扇形,颜色分 别为红黄绿三种,指针的位置固定,转动盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向黄色的概率为$\frac{2}{7}$.
如图,一个转盘被分成7个相同的扇形,颜色分 别为红黄绿三种,指针的位置固定,转动盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向黄色的概率为$\frac{2}{7}$.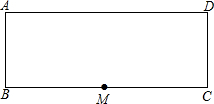 如图是矩形纸片ABCD.AB=16cm,BC=40cm,M是边BC的中点,沿过M的直线翻折.若点B恰好落在边AD上,那么折痕长度为10$\sqrt{5}$或8$\sqrt{5}$cm.
如图是矩形纸片ABCD.AB=16cm,BC=40cm,M是边BC的中点,沿过M的直线翻折.若点B恰好落在边AD上,那么折痕长度为10$\sqrt{5}$或8$\sqrt{5}$cm.