题目内容
13．某工厂计划生产A，B两种产品共10件，其生产成本和利润如下表| A种产品 | B种产品 | |
| 成本（万元╱件） | 2 | 5 |
| 利润（万元╱件） | 1 | 3 |
（2）若工厂计划投入资金不多于26万元，问工厂有哪几种方案？
分析 （1）设生产A种产品x件，则生产B种产品有（10-x）件，根据计划获利14万元，即两种产品共获利14万元，即可列方程求解；
（2）根据计划投入资金不多于26万元，这两个不等关系即可列出不等式，求得x的范围，再根据x是非负整数，确定x的值，x的值的个数就是方案的个数．
解答 解：（1）设生产A产品x件，B产品y件．
由题意得：$\left\{\begin{array}{l}x+y=10\\ x+3y=14\end{array}\right.$，
解这个方程得：$\left\{\begin{array}{l}x=8\\ y=2\end{array}\right.$，
答：若工厂计划获利14万元，生产A产品8件，B产品2件．
（2）设生产A产品z件
由题意得：2z+5（10-z）≤26，
解得：z≥8．
因为8≤z≤10，且z为整数．
所以z=8，z=9，z=10．
方案一：生产A产品8件，B产品2件
方案二：生产A产品9件，B产品1件
方案三：生产A产品10件．
点评 本题考查了二元一次方程的应用，一元一次不等式的应用．解决问题的关键是读懂题意，找到关键描述语，进而找到所求的量的数量关系．
练习册系列答案
相关题目
4．下列计算中，正确的是（ ）
| A． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B． | $2+\sqrt{2}=2\sqrt{2}$ | C． | $\sqrt{6}÷2=\sqrt{3}$ | D． | $3\sqrt{2}-\sqrt{2}=2\sqrt{2}$ |
1．若a＞b，则下列式子正确的是（ ）
| A． | a-6＞b-2 | B． | -5a＞-5b | C． | 4+3a＞4+3b | D． | ac＞bc |
如图，已知AB∥CD，∠E=80°，∠B=30°，求∠C的度数．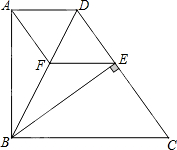
如图，在直角梯形ABCD中，AD∥BC，AB⊥AD，BC=CD，BE⊥CD，垂足为E，点F在BD上，连接AF、EF．
2．下列运算正确的是（ ）
| A． | x3+x3=x6 | B． | x6÷x2=x4 | C． | xm•xn=xmn | D． | -x5•x4=x9 |
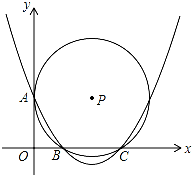已知：如图，在平面直角坐标系xOy中，点A（0，$\sqrt{3}$），点B（1，0），点C（3，0），以点P为圆心的圆与y轴相切于点A，与x轴相交于B、C两点（点B在点C的左边）．