题目内容
4.下列计算中,正确的是( )| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $2+\sqrt{2}=2\sqrt{2}$ | C. | $\sqrt{6}÷2=\sqrt{3}$ | D. | $3\sqrt{2}-\sqrt{2}=2\sqrt{2}$ |
分析 根据二次根式的加减法对各选项进行逐一分析即可.
解答 解:A、$\sqrt{2}$与$\sqrt{3}$不是同类项,不能合并,故本选项错误;
B、2与$\sqrt{2}$不是同类项,不能合并,故本选项错误;
C、$\sqrt{6}$÷2=$\sqrt{6}$÷$\sqrt{4}$=$\sqrt{\frac{3}{2}}$=$\frac{\sqrt{6}}{2}$,故本选项错误;
D、3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,故本选项正确.
故选D.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列各根式是最简二次根式的是( )
| A. | $\sqrt{15}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{54}$ | D. | $\sqrt{12}$ |
13.某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于26万元,问工厂有哪几种方案?
| A种产品 | B种产品 | |
| 成本(万元╱件) | 2 | 5 |
| 利润(万元╱件) | 1 | 3 |
(2)若工厂计划投入资金不多于26万元,问工厂有哪几种方案?
 将一副三角板按如图的位置摆放,则∠AOB=75°.
将一副三角板按如图的位置摆放,则∠AOB=75°.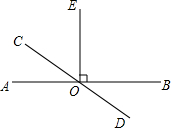 如图,直线AB、CD相交于点0,0E丄AB,且∠AOC=40°,若F为直线CD上任一点 (0点除外),则∠EOF的度数为50°或130°.
如图,直线AB、CD相交于点0,0E丄AB,且∠AOC=40°,若F为直线CD上任一点 (0点除外),则∠EOF的度数为50°或130°.