题目内容
5.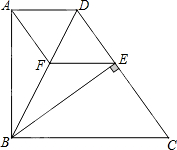 如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E,点F在BD上,连接AF、EF.
如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E,点F在BD上,连接AF、EF.(1)求证:DA=DE;
(2)如果AF∥CD,则四边形ADEF是什么特殊四边形?请证明你的结论.
分析 (1)利用平行线的性质结合全等三角形的判定方法得出△ABD≌△EBD(HL),进而得出DA=DE;
(2)首先得出AF=DE且AF∥CD,得出四边形ADEF为平行四边形,再利用菱形的判定方法得出答案.
解答 证明:(1)∵AD∥BC,∴∠DBC=∠ADB.
又∵BC=CD,∴∠DBC=∠BDC.
∴∠ADB=∠BDC.
又∵∠ADB=∠BDC,BA⊥AD,BE⊥CD,
∴BA=BE.
在RT△ABD和RT△EB中,
∵$\left\{\begin{array}{l}{BD=BD}\\{AB=BE}\end{array}\right.$
∴△ABD≌△EBD(HL),
∴AD=ED;
(2)结论:如果AF∥CD,则四边形ADEF是菱形,
理由:∵AF∥CD,∴∠BDC=∠AFD,
又∵∠ADB=∠BDC,
∴∠AFD=∠ADB,
∴AD=AF,
又∵AD=DE,∴AF=DE且AF∥CD,
∴四边形ADEF为平行四边形,
∵AD=DE,
∴四边形ADEF为菱形.
点评 此题主要考查了全等三角形的判定与性质以及平行四边形和菱形的判定,得出四边形ADEF为平行四边形是解题关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于26万元,问工厂有哪几种方案?
| A种产品 | B种产品 | |
| 成本(万元╱件) | 2 | 5 |
| 利润(万元╱件) | 1 | 3 |
(2)若工厂计划投入资金不多于26万元,问工厂有哪几种方案?
 将一副三角板按如图的位置摆放,则∠AOB=75°.
将一副三角板按如图的位置摆放,则∠AOB=75°.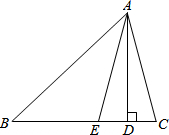 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=45°,∠C=75°,求∠DAE的度数.
如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=45°,∠C=75°,求∠DAE的度数. 如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,求△ADE的周长.
如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,求△ADE的周长.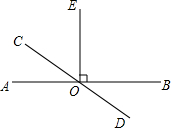 如图,直线AB、CD相交于点0,0E丄AB,且∠AOC=40°,若F为直线CD上任一点 (0点除外),则∠EOF的度数为50°或130°.
如图,直线AB、CD相交于点0,0E丄AB,且∠AOC=40°,若F为直线CD上任一点 (0点除外),则∠EOF的度数为50°或130°.