题目内容
8.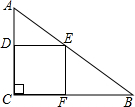 如图,正方形CDEF内接于Rt△ABC,点D、E、F分别在边AC、AB和BC上,当AD=2,BF=3时,正方形CDEF的面积是6.
如图,正方形CDEF内接于Rt△ABC,点D、E、F分别在边AC、AB和BC上,当AD=2,BF=3时,正方形CDEF的面积是6.
分析 根据正方形的性质得到DE∥BC,由平行线的性质得到∠AED=∠B,∠ADE=∠EFB=90°,推出△ADE∽△BEF,根据相似三角形的性质得到$\frac{AD}{EF}=\frac{DE}{BF}$,代入数据即可得到结论.
解答 解:∵四边形CDEF是正方形,
∴DE∥BC,
∴∠AED=∠B,∠ADE=∠EFB=90°,
∴△ADE∽△BEF,
∴$\frac{AD}{EF}=\frac{DE}{BF}$,
即$\frac{2}{EF}=\frac{DE}{3}$,
∴DE•EF=2×3=6,
∴正方形CDEF的面积是6.
故答案为:6.
点评 本题考查了相似三角形的判定和性质,正方形的性质,熟练掌握相似三角形的性质定理是解题的关键.

练习册系列答案
相关题目
16.下列说法不正确的是( )
| A. | 有一个角等于60°的两个等腰三角形相似 | |
| B. | 有一个底角等于30°的两个等腰三角形相似 | |
| C. | 有一个锐角相等的两个等腰三角形相似 | |
| D. | 有一个锐角相等的两个直角三角形相似 |
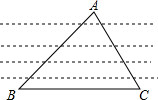 如图,为了测量河宽,在河的一边沿岸边选取B、C两点,在对岸岸边选择点A.测得∠B=45°,∠C=60°,BC=30米.求这条河的宽度(这里指点A到直线BC的距离).(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,为了测量河宽,在河的一边沿岸边选取B、C两点,在对岸岸边选择点A.测得∠B=45°,∠C=60°,BC=30米.求这条河的宽度(这里指点A到直线BC的距离).(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)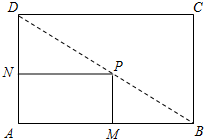 如图所示,在一矩形空地ABCD内建筑一个小的矩形花坛AMPN,要求P在BD上,M、N分别在AB、AD上.已知AB=160米,AD=100米,设AN=x(米).
如图所示,在一矩形空地ABCD内建筑一个小的矩形花坛AMPN,要求P在BD上,M、N分别在AB、AD上.已知AB=160米,AD=100米,设AN=x(米).