题目内容
13.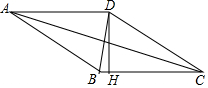 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥BC于H,则DH等于( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥BC于H,则DH等于( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | 5 | D. | 4 |
分析 设AC与BD交于点O.首先利用勾股定理求出BC,再利用菱形的面积公式求出DH即可.
解答 解:设AC与BD交于点O.
∵四边形ABCD是菱形,
∴AC⊥BD,
∴OB=OD=3,OC=OA=4,
在Rt△BOC中,BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵S菱形ABCD=$\frac{1}{2}$•AC•BD=BC•DH,
∴DH=$\frac{24}{5}$,
故选A.
点评 本题考查菱形的性质、勾股定理等知识,解题的关键是学会利用菱形的两种面积公式求菱形的高DH.

练习册系列答案
相关题目
8.如果(a-1)x2+ax+a2-1=0是关于x的一元二次方程,那么必有( )
| A. | a≠0 | B. | a≠1 | C. | a≠-1 | D. | a=±-1 |
18.将三角形、菱形、正方形、圆四种图形(大小不计)组合如图,观察并思考最后一图对应的数为( )


| A. | 13 | B. | 24 | C. | 31 | D. | 42 |
5.下列语句正确的是( )
| A. | 一条直线可以看成一个平角 | |
| B. | 周角是一条射线 | |
| C. | 角是由一条射线旋转而成的 | |
| D. | 角是由公共端点的两条射线组成的图形 |
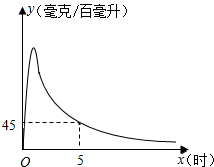 如图,实验数据显示,一般成年人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可以近似的用二次函数y=-200x2+400x刻画,1.5小时后(包括1.5小时)y与x可近似的用反比例函数y=$\frac{k}{x}$(k>0)刻画.
如图,实验数据显示,一般成年人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可以近似的用二次函数y=-200x2+400x刻画,1.5小时后(包括1.5小时)y与x可近似的用反比例函数y=$\frac{k}{x}$(k>0)刻画.