题目内容
11. 如图,在△ABC中,∠ACB=90°,CD是∠ACB的平分线,将△ABC绕点C按逆时针方向旋转,边AC落在直线CD上,得到△A1B1C1,A1B1交边BC于F.求证:CF+A1D=AC.
如图,在△ABC中,∠ACB=90°,CD是∠ACB的平分线,将△ABC绕点C按逆时针方向旋转,边AC落在直线CD上,得到△A1B1C1,A1B1交边BC于F.求证:CF+A1D=AC.
分析 根据旋转性质可得AC=A1C、BC=B1C、∠B=∠B1、∠BCB1=∠ACA1,再证△BCD≌△B1CF可得CD=CF,从而根据AC=A1C,即AC=CD+A1D即可得.
解答 证明:由旋转可得AC=A1C,BC=B1C,∠B=∠B1,∠BCB1=∠ACA1,
∵∠ACB=90°,CD是∠ACB的平分线,
∴∠BCD=∠BCB1=∠ACA1=45°,
在△BCD和△B1CF中,
∵$\left\{\begin{array}{l}{∠B=∠{B}_{1}}\\{BC={B}_{1}C}\\{∠BCD=∠{B}_{1}CF}\end{array}\right.$,
∴△BCD≌△B1CF(ASA),
∴CD=CF,
∵AC=A1C,即AC=CD+A1D,
∴CF+A1D=AC.
点评 本题主要考查旋转的性质和全等三角形的判定和性质,证明两三角形全等得到CD=CF是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 如图是某月份的日历表,任意框出同一列上的三个数,则这三个数的和不可能是( )
如图是某月份的日历表,任意框出同一列上的三个数,则这三个数的和不可能是( )
 如图是某月份的日历表,任意框出同一列上的三个数,则这三个数的和不可能是( )
如图是某月份的日历表,任意框出同一列上的三个数,则这三个数的和不可能是( )| A. | 39 | B. | 43 | C. | 57 | D. | 66 |
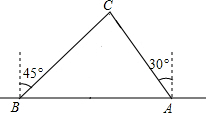 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域,如图,在B处测得C在东北方向上,在A处测得C在北偏西30°的方向上.
为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域,如图,在B处测得C在东北方向上,在A处测得C在北偏西30°的方向上.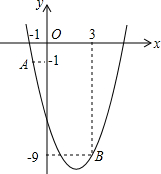 如图,已知抛物线y=ax2-4x+c的图象经过点A和点B.
如图,已知抛物线y=ax2-4x+c的图象经过点A和点B. 如图,已知在△ABC中,AB=AC,BD⊥AC,AE⊥BC.求证:∠DBC=$\frac{1}{2}$∠BAC.
如图,已知在△ABC中,AB=AC,BD⊥AC,AE⊥BC.求证:∠DBC=$\frac{1}{2}$∠BAC. 如图,已知⊙O是△ABC的内切圆,切点分别是D、E、F.若∠DOE=130°,∠C=60°,求∠A的度数.
如图,已知⊙O是△ABC的内切圆,切点分别是D、E、F.若∠DOE=130°,∠C=60°,求∠A的度数.