如果关于x的方程x2-3x+k=0有两个相等的实数根.那么实数k的值是$\frac{9}{4}$．题目和参考答案——青夏教育精英家教网—

题目内容

11．如果关于x的方程x²-3x+k=0有两个相等的实数根，那么实数k的值是$\frac{9}{4}$．

分析根据方程有两个相等的实数根结合根的判别式，即可得出关于k的一元一次方程，解方程即可得出结论．

解答解：∵关于x的方程x²-3x+k=0有两个相等的实数根，
∴△=（-3）²-4×1×k=9-4k=0，
解得：k=$\frac{9}{4}$．
故答案为：$\frac{9}{4}$．

点评本题考查了根的判别式以及解一元一次方程，解题的关键是找出9-4k=0．本题属于基础题，难度不大，解决该题型题目时，根据方程解的情况结合根的判别式得出方程（不等式或不等式组）是关键．

练习册系列答案

相关题目

1．

如图，已知抛物线y=x²+bx与直线y=2x+4交于A（a，8）、B两点，点P是抛物线上A、B之间的一个动点，过点P分别作x轴、y轴的平行线与直线AB交于点C和点E．
（1）求抛物线的解析式；
（2）若C为AB中点，求PC的长；
（3）如图，以PC，PE为边构造矩形PCDE，设点D的坐标为（m，n），请求出m，n之间的关系式．

2．三个连续正整数的和小于39，这样的正整数中，最大一组的和是（　　）

19．已知：在平行四边形ABCD中，点E在直线AD上，AE=$\frac{1}{3}$AD，连接CE交BD于点F，则EF：FC的值是$\frac{2}{3}$或$\frac{4}{3}$．

6．

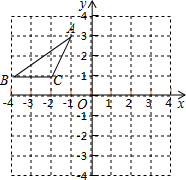如图，在平面直角坐标系中，点A、B、C的坐标分别为（-1，3）、（-4，1）（-2，1），先将△ABC沿一确定方向平移得到△A₁B₁C₁，点B的对应点B₁的坐标是（1，2），再将△A₁B₁C₁绕原点O顺时针旋转90°得到△A₂B₂C₂，点A₁的对应点为点A₂．
（1）画出△A₁B₁C₁；
（2）画出△A₂B₂C₂；
（3）求出在这两次变换过程中，点A经过点A₁到达A₂的路径总长．

16．

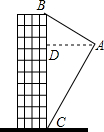如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为30°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为90米，那么该建筑物的高度BC约为208米．（精确到1米，参考数据：$\sqrt{3}$≈1.73）

3．已知正比例函数y=3x的图象经过点（1，m），则m的值为（　　）

20．不等式组$\left\{\begin{array}{l}{2x+2＞x}\\{3x＜x+2}\end{array}\right.$的解集是（　　）

8．

如图，在△ABC中，AD是∠BAC的平分线，AD的垂直平分线交BC的延长线于点F．
（1）求证：∠FAD=∠FDA；
（2）若∠B=50°，求∠CAF的度数．

试题分类