题目内容
19.已知:在平行四边形ABCD中,点E在直线AD上,AE=$\frac{1}{3}$AD,连接CE交BD于点F,则EF:FC的值是$\frac{2}{3}$或$\frac{4}{3}$.分析 分两种情况:①当点E在线段AD上时,由四边形ABCD是平行四边形,可证得△EFD∽△CFB,求出DE:BC=2:3,即可求得EF:FC的值;
②当点E在射线DA上时,同①得:△EFD∽△CFB,求出DE:BC=4:3,即可求得EF:FC的值.
解答 解:∵AE=$\frac{1}{3}$AD,
∴分两种情况:
①当点E在线段AD上时,如图1所示
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△EFD∽△CFB,
∴EF:FC=DE:BC,
∵AE=$\frac{1}{3}$AD,
∴DE=2AE=$\frac{2}{3}$AD=$\frac{2}{3}$BC,
∴DE:BC=2:3,
∴EF:FC=2:3;
②当点E在线段DA的延长线上时,如图2所示:
同①得:△EFD∽△CFB,
∴EF:FC=DE:BC,
∵AE=$\frac{1}{3}$AD,
∴DE=4AE=$\frac{4}{3}$AD=$\frac{4}{3}$BC,
∴DE:BC=4:3,
∴EF:FC=4:3;
综上所述:EF:FC的值是$\frac{2}{3}$或$\frac{4}{3}$;
故答案为:$\frac{2}{3}$或$\frac{4}{3}$.
点评 此题考查了相似三角形的判定与性质与平行四边形的性质.此题难度不大,证明三角形相似是解决问题的关键;注意分情况讨论.

练习册系列答案
相关题目
9. 图中是一个少数名族手鼓的轮廓图,其主视图是( )
图中是一个少数名族手鼓的轮廓图,其主视图是( )
 图中是一个少数名族手鼓的轮廓图,其主视图是( )
图中是一个少数名族手鼓的轮廓图,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
4.关于x的分式方程$\frac{2x-m}{x+1}$=3的解是正数,则字母m的取值范围是( )
| A. | m>3 | B. | m<3 | C. | m>-3 | D. | m<-3 |
8.超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )
| A. | 0.8x-10=90 | B. | 0.08x-10=90 | C. | 90-0.8x=10 | D. | x-0.8x-10=90 |
 如图,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB请你添加一个条件EB=DC,使四边形DBCE是矩形.
如图,在平行四边形ABCD中,延长AD到点E,使DE=AD,连接EB,EC,DB请你添加一个条件EB=DC,使四边形DBCE是矩形.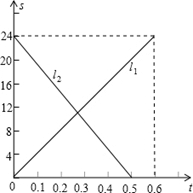 甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)的函数关系,则下列说法:
甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)的函数关系,则下列说法: