题目内容
16.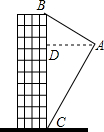 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为208米.(精确到1米,参考数据:$\sqrt{3}$≈1.73)
如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为208米.(精确到1米,参考数据:$\sqrt{3}$≈1.73)
分析 分别利用锐角三角函数关系得出BD,DC的长,进而求出该建筑物的高度.
解答 解:由题意可得:tan30°=$\frac{BD}{AD}$=$\frac{BD}{90}$=$\frac{\sqrt{3}}{3}$,
解得:BD=30$\sqrt{3}$,
tan60°=$\frac{DC}{AD}$=$\frac{DC}{90}$=$\sqrt{3}$,
解得:DC=90$\sqrt{3}$,
故该建筑物的高度为:BC=BD+DC=120$\sqrt{3}$≈208(m),
故答案为:208.
点评 此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
4.关于x的分式方程$\frac{2x-m}{x+1}$=3的解是正数,则字母m的取值范围是( )
| A. | m>3 | B. | m<3 | C. | m>-3 | D. | m<-3 |
8.超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )
| A. | 0.8x-10=90 | B. | 0.08x-10=90 | C. | 90-0.8x=10 | D. | x-0.8x-10=90 |
13.已知矩形一边的长为5,另一边的长为4,则它的对角线的长为( )
| A. | 3 | B. | $\sqrt{41}$ | C. | 4 | D. | 2$\sqrt{41}$ |
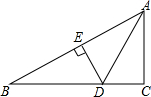 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( ) 把一个正六棱柱如图1摆放,光线由上向下照射此正六棱柱时的正投影是( )
把一个正六棱柱如图1摆放,光线由上向下照射此正六棱柱时的正投影是( )



 如图,在菱形ABCD中,AB=5,AC=8,则菱形的面积是24.
如图,在菱形ABCD中,AB=5,AC=8,则菱形的面积是24.