题目内容
6.下列实数中,为无理数的是( )| A. | -2 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答 解:A、-2是整数,是有理数,选项不符合题意;
B、$\sqrt{2}$是无理数,选项符合题意;
C、2是整数,是有理数,选项不符合题意;
D、4是整数,是有理数,选项不符合题意.
故选B.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.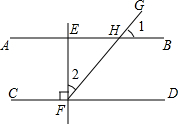 如图,直线AB∥CD,EF⊥CD,垂足为F,交AB于点E,射线FG交AB于点H.若∠1=30°,则∠2的度数为( )
如图,直线AB∥CD,EF⊥CD,垂足为F,交AB于点E,射线FG交AB于点H.若∠1=30°,则∠2的度数为( )
 如图,直线AB∥CD,EF⊥CD,垂足为F,交AB于点E,射线FG交AB于点H.若∠1=30°,则∠2的度数为( )
如图,直线AB∥CD,EF⊥CD,垂足为F,交AB于点E,射线FG交AB于点H.若∠1=30°,则∠2的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
17. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
1.下列各运算中,计算正确的是( )
| A. | (x-2)2=x2-4 | B. | (3a2)3=9a6 | C. | x6÷x2=x3 | D. | x3•x2=x5 |
2.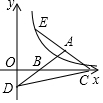 如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y=$\frac{k}{x}$(x>0)的图象过点E.若△BCD的面积为2$\sqrt{2}$,则k的值为( )
如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y=$\frac{k}{x}$(x>0)的图象过点E.若△BCD的面积为2$\sqrt{2}$,则k的值为( )
 如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y=$\frac{k}{x}$(x>0)的图象过点E.若△BCD的面积为2$\sqrt{2}$,则k的值为( )
如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y=$\frac{k}{x}$(x>0)的图象过点E.若△BCD的面积为2$\sqrt{2}$,则k的值为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
3.若分式$\frac{{{x^2}-1}}{{{x^2}-2x-3}}$的值为0,则x的值为( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
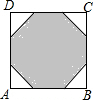 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是8+8$\sqrt{2}$.
如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是8+8$\sqrt{2}$.