Question

5．已知⊙A和⊙B相交于C、D．且它们都与⊙O内切，切点分别为M（M在⊙A上）、N．射线CD交⊙O于点P．PM交⊙A于点E，PN交⊙B于点F，求证：EF是⊙A、⊙B的公切线．

Answer 1

分析 如图，连接OP、OM、ON、MN、AE、BF，则O、A、M共线，O、B、N共线．只要证明∠PFE+∠4=90°，BF∥AE即可解决问题．

解答 证明：如图，连接OP、OM、ON、MN、AE、BF，则O、A、M共线，O、B、N共线．
∵OP=ON=OM，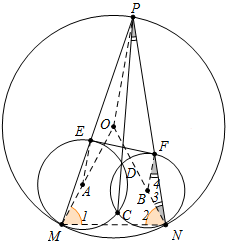
∴∠1=∠2，∠OPN=∠3，∠OMP=∠OPM，
∵2∠OMP+2∠1+2∠3=180°
∴∠OMP+∠1+∠3=90°，
∵PD•PC=PE•PM=PF•PN，
∴$\frac{PF}{PM}$=$\frac{PE}{PN}$，∵∠EPF=∠NPM，
∴△PEF∽△PNM，
∴∠PFE=∠PMN，
∵BF=BN，
∴∠3=∠4，
∴∠PFE+∠4=∠OMP+∠1+∠3=90°，
∴∠EFB=90°，
∵AM=AE，OM=OP，
∴∠AME=∠AEM=∠OPM，
∴AE∥OP，同理BF∥OP，
∴AE∥BF，
∴∠AEF+∠EFB=180°，
∴∠FEA=∠EFB=90°，
∴EF是⊙A，⊙B的公切线．

点评 本题考查切线的判定、圆的有关知识、三角形内角和定理，平行线的性质等知识，解题的关键是学会添加常用辅助线，构造等腰三角形解决问题，题目比较难，辅助线比较多，属于竞赛题目．