题目内容
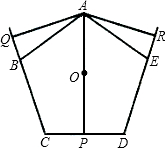 如图,ABCDE是正五边形,从顶点A向三边BC、CD、DE(或其延长线)作垂线AQ、AP、AR、(Q、P、R是垂足),O是此五边形的中心,若OP=1,求AO+AQ+AR的值.
如图,ABCDE是正五边形,从顶点A向三边BC、CD、DE(或其延长线)作垂线AQ、AP、AR、(Q、P、R是垂足),O是此五边形的中心,若OP=1,求AO+AQ+AR的值.考点:三角形的面积
专题:计算题
分析:先连接AC、AD、OC、OD,设正五边形ABCDE边长为a,由于SABCDE=S△ABC+S△ACD+S△ADE=5S△OCD,
即
AQ•a+
AP•a+
AR•a=5×
×1×a,化简得AQ+AP+AR=5,又AP=AO+OP,OP=1,易求AQ+AO+AR=4.
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:如图,连AC、AD、OC、OD,设正五边形ABCDE边长为a,
解:如图,连AC、AD、OC、OD,设正五边形ABCDE边长为a,
∵SABCDE=S△ABC+S△ACD+S△ADE=5S△OCD,
∴
AQ•a+
AP•a+
AR•a=5×
×1×a,
∴AQ+AP+AR=5,
又∵AP=AO+OP,
∴AQ+AO+AR=4.
 解:如图,连AC、AD、OC、OD,设正五边形ABCDE边长为a,
解:如图,连AC、AD、OC、OD,设正五边形ABCDE边长为a,∵SABCDE=S△ABC+S△ACD+S△ADE=5S△OCD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AQ+AP+AR=5,
又∵AP=AO+OP,
∴AQ+AO+AR=4.
点评:本题考查了正五边形的性质、三角形面积.注意五个顶点和中心的连线,分成的五个三角形全等.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
用10根长度相同的木棍拼成一个三角形(不剩余木棍也不折断木棍),则只能拼成( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
小李年初向建设银行贷款5万元用于购房,年利率为5%,按复利计算,若这笔借款分15次等额归还,每年1次,15年还清,并从借后次年年初开始归还,问每年应还大约( )
| A、4819元 |
| B、4818元 |
| C、4817元 |
| D、4816元 |
设菱形的周长为20,两条对角线的长是方程x2-(2m-1)x+4m-4=0的两个根,则m的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
| D、以上答案都不对 |
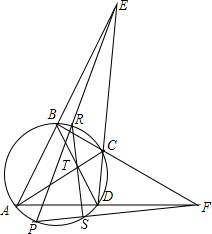 如图,四边形ABCD内接于圆,AB,DC延长线交于E,AD、BC延长线交于F,P为圆上任意一点,PE,PF分别交圆于R,S.若对角线AC与BD相交于T.求证:R,T,S三点共线.
如图,四边形ABCD内接于圆,AB,DC延长线交于E,AD、BC延长线交于F,P为圆上任意一点,PE,PF分别交圆于R,S.若对角线AC与BD相交于T.求证:R,T,S三点共线. 为了庆祝国庆,学校准备在教学楼大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为lm,高为3m.如果要求彩带从柱子底端的A处绕柱子4圈后到达柱子顶端的B处,那么至少应购买彩带
为了庆祝国庆,学校准备在教学楼大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为lm,高为3m.如果要求彩带从柱子底端的A处绕柱子4圈后到达柱子顶端的B处,那么至少应购买彩带 在一个立方体的八个顶点分别写上数字1,2,3,…,8,使得六个面的顶点上的数字分别为
在一个立方体的八个顶点分别写上数字1,2,3,…,8,使得六个面的顶点上的数字分别为