题目内容
19.已知关于x的-元二次方程x2+(4m+1)x+2m-1=0.(1)求证:该方程总有两个不相等的实数根;
(2)设该方程的两个根为x1,x2,是否存在实数m,使x1=2x2?
分析 (1)要证明方程总有两个不相等的实数根,那么只要证明△>0即可.
(2)根据根与系数的关系可知x1+x2=-(4m+1),结合x1x2=2m-1,由x1=2x2得到方程,求出m的值即可.
解答 (1)证明:△=(4m+1)2-4(2m-1)
=16m2+8m+1-8m+4=16m2+5>0,
∴不论m为任何实数,方程总有两个不相等的实数根.
(2)∵该方程的两个根为x1,x2,
∴x1+x2=-(4m+1),x1x2=2m-1,
∵x1=2x2,
∴-$\frac{1}{3}$(4m+1)=$\sqrt{\frac{2m-1}{2}}$
则32m2-2m+11=0,
此方程无解.
不存在实数m,使x1=2x2.
点评 本题考查了一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.以及根与系数的关系.

练习册系列答案
相关题目
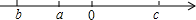 已知a,b,c在数轴上的位置如图所示,确定下列各式与0的大小关系.
已知a,b,c在数轴上的位置如图所示,确定下列各式与0的大小关系.