题目内容
10.如果关于x的方程(m-2)x2-2(m-1)x+m=0有两个相等的实数根,那么方程mx2-(m+2)x+(4-m)=0的根的情况是有两个不相等的实数根.分析 根据关于x的方程(m-2)x2-2(m-1)x+m=0有两个相等的实数根得出m的z值,进一步利用m的取值,判断方程mx2-(m+2)x+(4-m)=0的根的判别式的符号,得出答案即可.
解答 解:∵关于x的方程(m-2)x2-2(m-1)x+m=0有两个相等的实数根,
∴△=(2m-1)2-4m(m-2)=0,
解得:m=-$\frac{1}{4}$
∵方程mx2-(m+2)x+(4-m)=0,
∴△=(m+2) 2-4m(4-m)=5m2-12m+4=7$\frac{5}{16}$>0
∴方程有两个不相等的实数根.
故答案为:有两个不相等的实数根.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.

练习册系列答案
相关题目
20.已知关于x的方程2x2+6x+c=0的一个根是另一个根的2倍,则c的值为( )
| A. | 2 | B. | 4 | C. | -4 | D. | 8 |
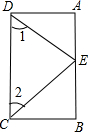 如图,CB⊥AB,CE平分∠BCD,DE平分∠ADC,DE=CE.∠1+∠2=90°.试说明:AB∥CD.
如图,CB⊥AB,CE平分∠BCD,DE平分∠ADC,DE=CE.∠1+∠2=90°.试说明:AB∥CD. 如图,CD为Rt△ABC斜边AB上的高,G为DC延长线上一点,AF⊥BG,垂足为F.AF交CD于E,求证:CD2=DE•DG.
如图,CD为Rt△ABC斜边AB上的高,G为DC延长线上一点,AF⊥BG,垂足为F.AF交CD于E,求证:CD2=DE•DG.