题目内容
11.已知抛物线y=a(x+2)2-1交x轴于A,B两点(A点在B点的左边)且AB=2,求解析式.分析 根据抛物线与x轴的交点间的距离公式和抛物线上点的坐标特征得到方程$\frac{\sqrt{a}}{a}$=1,解方程求得a即可.
解答 解:∵抛物线y=a(x+2)2-1交x轴于A,B两点,
∴0=a(x+2)2-1,
解得:x1=-2+$\frac{\sqrt{a}}{a}$,x2=-2-$\frac{\sqrt{a}}{a}$,
∵A点在B点的左边,且AB=2
∴2×$\frac{\sqrt{a}}{a}$=2
解得:a=0,或a=1,
a=0不合题意,舍去,
∴抛物线y=(x+2)2-1.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
20.已知关于x的方程2x2+6x+c=0的一个根是另一个根的2倍,则c的值为( )
| A. | 2 | B. | 4 | C. | -4 | D. | 8 |
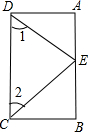 如图,CB⊥AB,CE平分∠BCD,DE平分∠ADC,DE=CE.∠1+∠2=90°.试说明:AB∥CD.
如图,CB⊥AB,CE平分∠BCD,DE平分∠ADC,DE=CE.∠1+∠2=90°.试说明:AB∥CD.