Question

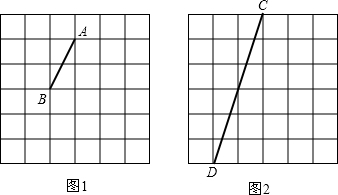
12．如图，四边形BCDE是正方形，数轴上点A表示的实数是1-$\sqrt{2}$．

Answer 1

分析 先根据正方形的性质得出CD=BC=1，∠BCD=90°，再利用勾股定理求出BD，那么AB=BD，然后根据两点间的距离公式即可得出点A表示的实数．

解答 解：∵四边形BCDE是正方形，
∴CD=BC=2-1=1，∠BCD=90°，
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{2}$，
∴AB=BD=$\sqrt{2}$，
∵点B表示的实数是1，A在B的左边，
∴点A表示的实数是1-$\sqrt{2}$．
故答案为1-$\sqrt{2}$．

点评 本题考查了实数与数轴，正方形的性质，勾股定理，两点间的距离公式，求出AB的长度是解题的关键．