题目内容
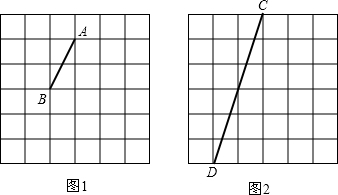
1.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫格点,图1,图2中分别有线段AB和线段CD,点A、B、C、D均在格点上.(1)在图1中画出以AB为腰的等腰三角形ABE,使点E在格点上,且tan∠BAE=$\frac{1}{2}$;
(2)在图2中画出以CD为边的直角三角形CDF,点F在格点上,使三角形CDF的面积为等腰三角形ABE面积的5倍,并在CF找一点G(点G在格点上),且使DG平分三角形CDF的面积.
分析 (1)根据AB为腰,tan∠BAE=$\frac{1}{2}$画出图象即可.
(2)根据△CDF是直角三角形,面积为10=$\frac{1}{2}$$•5\sqrt{2}$•5$\sqrt{2}$即可画出图象.
解答 解:(1)△ABE如图1所示,
(2)△CDF如图2所示,DG平分△CDF的面积.
点评 本题考查作图-设计与应用,解题的关键是根据面积10=$\frac{1}{2}$•5$\sqrt{2}$•5$\sqrt{2}$,找到5$\sqrt{2}$的线段,是数形结合的好题目,本题还考查学生的动手能力,属于中考常考题型.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
11.若x2+3x-5的值为7,则3x2+9x-2的值为( )
| A. | 5 | B. | 16 | C. | 21 | D. | 34 |
 如图,四边形BCDE是正方形,数轴上点A表示的实数是1-$\sqrt{2}$.
如图,四边形BCDE是正方形,数轴上点A表示的实数是1-$\sqrt{2}$.
 如图,直线y1=x+2与双曲线y2=$\frac{k}{x}$交于A(m,4),B(-4,n).
如图,直线y1=x+2与双曲线y2=$\frac{k}{x}$交于A(m,4),B(-4,n).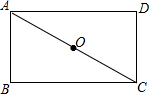 如图,矩形ABCD中,O为AC的中点,△ADC是否可由△CBA旋转得到?若能,请指出旋转中心和旋转角度;若不能,请说明理由.
如图,矩形ABCD中,O为AC的中点,△ADC是否可由△CBA旋转得到?若能,请指出旋转中心和旋转角度;若不能,请说明理由.