题目内容
12.先化简,再求值:$\frac{a}{a-1}÷\frac{{{a^2}-a}}{{{a^2}-1}}-\frac{1}{a-1}$,其中a=2.分析 利用平方差公式和分解因式等方法将原分式化简成$\frac{a}{a-1}$,并找出a的取值范围,再将a=2代入化简后的分式中即可得出结论.
解答 解:原式=$\frac{a}{a-1}$÷$\frac{a(a-1)}{(a+1)(a-1)}$-$\frac{1}{a-1}$,
=$\frac{a}{a-1}$•$\frac{a+1}{a}$-$\frac{1}{a-1}$,
=$\frac{a+1}{a-1}$-$\frac{1}{a-1}$,
=$\frac{a}{a-1}$.
∵a(a+1)(a-1)≠0,
∴a≠0且a≠±1.
当a=2时,原式=$\frac{a}{a-1}$=$\frac{2}{2-1}$=2.
点评 本题考查了分式的化简求值,解题的关键是将原分式化简成$\frac{a}{a-1}$.本题属于基础题,难度不大,解决该题型题目时,先对原分式进行化简,再将给定的数值代入化简后的分式(或整式)中求出结果即可.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
3.下列运算中正确的是( )
| A. | a5÷a5=0 | B. | a6×a4=a24 | C. | (x2-y2)2=x4-y4 | D. | (x3)3=x9 |
7.若分式$\frac{{x}^{2}-4}{x+2}$的值为0,则x的值为( )
| A. | -2 | B. | 2 | C. | 4 | D. | 2和-2 |
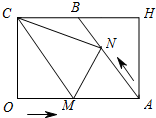 如图,在矩形OAHC中,OC=4,OA=6,B为CH中点,连接AB.动点M从点O出发沿OA边向点A运动;动点N从点A出发沿AB边向点B运动,两个动点同时出发,速度都是每秒1个单位长度,连接CM,CN,MN,设运动时间为t(秒)(0<t<5).解答下列问题:
如图,在矩形OAHC中,OC=4,OA=6,B为CH中点,连接AB.动点M从点O出发沿OA边向点A运动;动点N从点A出发沿AB边向点B运动,两个动点同时出发,速度都是每秒1个单位长度,连接CM,CN,MN,设运动时间为t(秒)(0<t<5).解答下列问题: