题目内容
10. 在平面直角坐标系xOy中,对于点P(x,y)(x≥0)的每一个整数点,给出如下定义:如果P'($\sqrt{|x|}$,$\sqrt{|y|}$)也是整数点,则称点P'为点P的“整根点”.例如:点(25,36)的“整根点”为点(5,6).
在平面直角坐标系xOy中,对于点P(x,y)(x≥0)的每一个整数点,给出如下定义:如果P'($\sqrt{|x|}$,$\sqrt{|y|}$)也是整数点,则称点P'为点P的“整根点”.例如:点(25,36)的“整根点”为点(5,6).(1)点A(4,8),B(0,16),C(25,-9)的整根点是否存在,若存在请写出整根点的坐标B′(0,4),C′(5,3);
(2)如果点M对应的整根点M'的坐标为(2,3),则点M的坐标M(4,9)或M(4,-9);
(3)在坐标系内有一开口朝下的二次函数y=ax2+4x(a≠0),如果在第一象限内的二次函数图象内部(不在图象上),若存在整根点的点只有三个,请求出实数a的取值范围.
分析 (1)、(2)根据“整根点”的定义进行解答;
(3)需要分类讨论:①当图象经过(4,4)时,如图:根据轴对称性,此时恰有1个整根点在图象上,2个整根点在图象内部,将其代入函数解析式即可求得a的值;
②当图象过(4,9)时,代入表达式得:9=16a+16,求得a的值.
综合①②即可求得a的取值范围.
解答 解:(1)A不存在整根点;
因为B′($\sqrt{|0|}$,$\sqrt{|16|}$)即(0,4)也是整数点,
所以B点的整根点坐标是B′(0,4).
同理C点的整根点坐标是C′(5,3).
故答案是:B′(0,4),C′(5,3);
(2)设M(x,y)(x≥0)依题意得:M'($\sqrt{|x|}$,$\sqrt{|y|}$),
∵M'(2,3),
∴M(4,9)或M(4,-9);
故答案是:M(4,9)或M(4,-9);
(3)由于图象开口向下,根据表达式特点及对称轴所在位置的变化,将分为以下两种情况进行讨论:
当图象经过(4,4)时,如图:根据轴对称性,此时恰有1个整根点在图象上,2个整根点在图象内部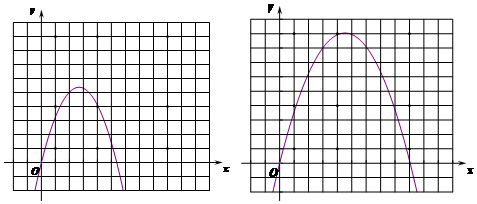
因此:代入表达式得:4=16a+16
解得a=$-\frac{3}{4}$;
当图象过(4,9)时,代入表达式得:9=16a+16
解得a=$-\frac{7}{16}$
根据图象的轴对称性可以验证(1,4)(9,1)都不在图象内部,
因此此时有3个整根点在图象内部;
综合上述分析当$-\frac{3}{4}<a≤-\frac{7}{16}$.
点评 此题是二次函数综合题,主要考查了新定义,待定系数法,二次函数图象上点的坐标特征等知识点;解本题的关键是理解“整根点”的定义.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
5.在同一平面内,下列说法正确的是( )
| A. | 两点之间的距离就是两点间的线段 | |
| B. | 与同一条直线垂直的两条直线也垂直 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 过一点有且只有一条直线与已知直线垂直 |
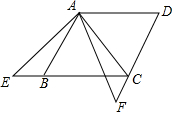 如图,四边形ABCD是菱形,AB=4,∠ABC=60°,E,F分别在CB,DC的延长线上,且∠EAF=60°,∠EAB=15°,则S△ACF=6-2$\sqrt{3}$.
如图,四边形ABCD是菱形,AB=4,∠ABC=60°,E,F分别在CB,DC的延长线上,且∠EAF=60°,∠EAB=15°,则S△ACF=6-2$\sqrt{3}$.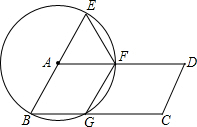 如图,平行四边形ABCD中,以A为圆心,AB为半径的圆分别交AD、BC于F、G,延长BA交圆于E.
如图,平行四边形ABCD中,以A为圆心,AB为半径的圆分别交AD、BC于F、G,延长BA交圆于E. 如图,ABC三点在同一条直线上,且∠1=∠2,∠3=∠D,试判断BD与CE的位置关系,并说明理由.
如图,ABC三点在同一条直线上,且∠1=∠2,∠3=∠D,试判断BD与CE的位置关系,并说明理由. 请认真观察图形,解答下列问题:
请认真观察图形,解答下列问题:
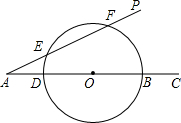 如图:∠PAC=30°,AD=3,BD=10,以BD为直径的交AP于E、F,求圆心O到AP的距离及EF长.
如图:∠PAC=30°,AD=3,BD=10,以BD为直径的交AP于E、F,求圆心O到AP的距离及EF长.