题目内容
17.现有一块直角三角形的铁皮ABC,∠ACB=90°,AC=80,BC=60,要在其中剪出一个面积尽可能大的正方形,小红和小亮各想出了甲,乙两种方案,请你帮忙算一算哪一种方案剪出的正方形面积较大?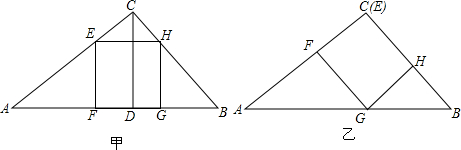
分析 对于方案甲:先利用勾股定理计算出AB=100,再利用面积法计算出CD=48,设正方形EFGH的边长为x,则EF=EH=MD=x,证明△CEH∽△CAB,然后利用相似比可计算出x=$\frac{1200}{37}$;对于方案乙:设正方形EFGH的边长为y,则EF=FG=y,AF=80-y,证明△AGF∽△ABC,利用相似比可计算出y=$\frac{240}{7}$,然后比较x和y的大小即可判断哪一种方案剪出的正方形面积较大.
解答 解:方案甲:AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{6{0}^{2}+8{0}^{2}}$=100,
∵$\frac{1}{2}$CD•AB=$\frac{1}{2}$AC•BC,
∴CD=$\frac{60×80}{100}$=48,
设正方形EFGH的边长为x,则EF=EH=MD=x,
∵EH∥AB,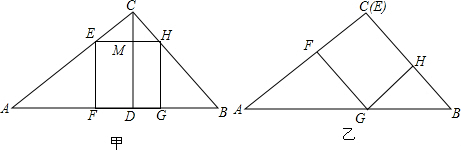
∴△CEH∽△CAB,
∴$\frac{EH}{AB}$=$\frac{CM}{CD}$,即$\frac{x}{100}$=$\frac{48-x}{48}$,解得x=$\frac{1200}{37}$;
方案乙:设正方形EFGH的边长为y,则EF=FG=y,AF=80-y,
∵FG∥BC,
∴△AGF∽△ABC,
∴$\frac{FG}{BC}$=$\frac{AF}{AC}$,即$\frac{y}{60}$=$\frac{80-y}{80}$,解得y=$\frac{240}{7}$,
∵$\frac{240}{7}$=$\frac{1200}{35}$>$\frac{1200}{37}$,
即x<y,
∴方案乙剪出的正方形面积较大.
点评 本题考查了相似三角形的应用:常常构造“A”型或“X”型相似图,然后利用三角形相似的性质求相应线段的长.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案 在⊙O中,弦AC⊥BD,垂足为P.过点P的直线和AB垂直于H,交CD于M.求证:MC=MD.
在⊙O中,弦AC⊥BD,垂足为P.过点P的直线和AB垂直于H,交CD于M.求证:MC=MD.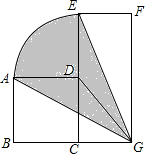 已知正方形ABCD的边长为a,长方形CEFG的边CE长为2a,边CG长为b.求以D为圆心,AD为半径的弧与GA,GE所围成的阴影部分的面积(用含a,b的代数式表示).
已知正方形ABCD的边长为a,长方形CEFG的边CE长为2a,边CG长为b.求以D为圆心,AD为半径的弧与GA,GE所围成的阴影部分的面积(用含a,b的代数式表示).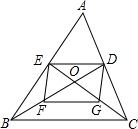 如图所示,在△ABC中,中线BD、CE相交于点0,点F、G分别为0B、OC的中点,求证:O是线段EG、DF的中点.
如图所示,在△ABC中,中线BD、CE相交于点0,点F、G分别为0B、OC的中点,求证:O是线段EG、DF的中点.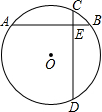 如图,在⊙O中,弦AB⊥CD于E,已知AE=5,CE=1,BE=3.求⊙O的半径.
如图,在⊙O中,弦AB⊥CD于E,已知AE=5,CE=1,BE=3.求⊙O的半径.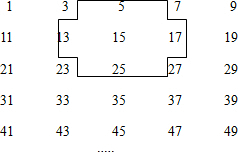 将连续奇数1,3,5,7,…排成如图所示的数表.
将连续奇数1,3,5,7,…排成如图所示的数表.