Question

7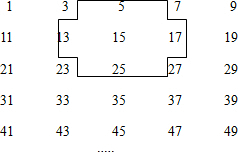．将连续奇数1，3，5，7，…排成如图所示的数表．
（1）十字形框中的五个数之和与中间数15有什么关系？
（2）设中间数为a，如何用代数式表示十字形框中五个数之和？
（3）若将十字形框上下左右移动，可框住另外五个数，这五个数还有上述的规律吗？
（4）十字框中的五个数之和能等于2012吗？能等于2015吗？能等于2075吗？

Answer 1

分析 （1）先求出这5个数的和，用这个和去除以中间的这个数15就可以得出结论；
（2）由左右相邻两个奇数之间相差2，上下相邻两个奇数之间相差10，就可以分别表示出这5个数，进而得出结论；
（3）同样设中间数为b，就可以表示出这5个数的和，得出结论与（1）一样；
（4）设中间的一个数为x，建立方程求出x的值就可以得出结论．

解答 解：（1）由题意，得
5+13+15+17+25=75．
75÷15=5．
因此十字框中的五个数的和是中间数15的5倍；
（2）设中间数为a，则其余的4个数分别为a-2，a+2，a-10，a+10，由题意，得
a+a-2+a+2+a-10+a+10=5a．
答：5个数之和为5a；
（3）设设中间数为b，则其余的4个数分别为b-2，b+2，b-10，b+10，由题意，得
∵b+b-2+b+2+b-10+b+10=5b，
∴这五个数的和还是中间这个数的5倍；
（4）设中间的一个数为x，则其余的4个数分别为x-2，x+2，x-10，x+10，由题意，得
x+x-2+x+2+x-10+x+10=2012，
解得：x=402.4．
∵402.4是小数，
∴不存在十字框中五数之和等于2012，
同理5个数之和等于2015，解得x=403，403在第二列，可以得出5个数之和等于2015；
同理5个数之和等于2075，解得x=415，415在第三列，可以得出5个数之和等于2075．

点评 此题考查一元一次方程的实际运用，找出数字的排列规律，利用数字和建立方程求得答案即可．