题目内容
当n=1时,m=10;当n=2时,得m=19;当n=3时,m=30,根据其中规律可知:m可以用n表示为 .
考点:规律型:数字的变化类
专题:规律型
分析:观察不难发现,相邻两个数的差为连续的奇数,然后分别列出相邻两个数的差的算式,再相加求解即可.
解答:解:m1=10,
m2-m1=19-10=9,
m3-m2=30-19=11,
…,
mn-mn-1=2n+5,
∵mn=m1+(m2-m1)+(m3-m2)+…+(mn-mn-1)=10+9+11+…+(2n+5)=10+
=n2+6n+3,
∴m=n2+6n+3.
故答案为:m=n2+6n+3.
m2-m1=19-10=9,
m3-m2=30-19=11,
…,
mn-mn-1=2n+5,
∵mn=m1+(m2-m1)+(m3-m2)+…+(mn-mn-1)=10+9+11+…+(2n+5)=10+
| (n-1)(9+2n+5) |
| 2 |
∴m=n2+6n+3.
故答案为:m=n2+6n+3.
点评:本题是对数字变化规律的考查,观察出相邻两个数的差是连续的奇数是解题的关键,难点在于表示出mn-mn-1=2n+5.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 根据输入的有理数,按图中程序计算,并把输出的结果填入表内.提示:要有适当的运算过程
根据输入的有理数,按图中程序计算,并把输出的结果填入表内.提示:要有适当的运算过程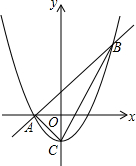 如图,抛物线y=x2-1的顶点为C,直线y=x+1与抛物线交于A,B两点.M是抛物线上一点,过M作MG⊥x轴,垂足为G.如果以A,M,G为顶点的三角形与△ABC相似,那么点M的坐标是
如图,抛物线y=x2-1的顶点为C,直线y=x+1与抛物线交于A,B两点.M是抛物线上一点,过M作MG⊥x轴,垂足为G.如果以A,M,G为顶点的三角形与△ABC相似,那么点M的坐标是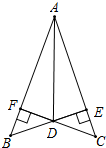 如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于 点D,DE=DF,连结AD.
如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于 点D,DE=DF,连结AD.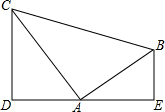 如图,已知AB⊥AC,AB=AC,DE过点A,且CD⊥DE,BE⊥DE,垂足分别为点D,E.
如图,已知AB⊥AC,AB=AC,DE过点A,且CD⊥DE,BE⊥DE,垂足分别为点D,E.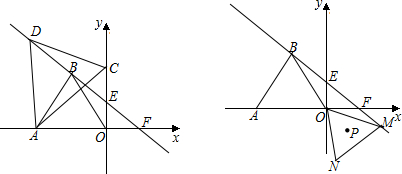
 已知:如图,AB=CD,AE=DF,且AE⊥BC于E,DF⊥BC于F.求证:∠B=
已知:如图,AB=CD,AE=DF,且AE⊥BC于E,DF⊥BC于F.求证:∠B=