Question

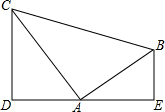如图，已知AB⊥AC，AB=AC，DE过点A，且CD⊥DE，BE⊥DE，垂足分别为点D，E．
（1）∠DCA与∠EAB相等吗？说明理由；
（2）△ADC与△BEA全等吗？说明理由．

Answer 1

考点：全等三角形的判定与性质

专题：常规题型

分析：（1）根据AB⊥AC和CD⊥DE可以求得∠DCA=∠EAB；
（2）根据（1）中的∠DCA=∠EAB和AB=AC可以求证△ADC≌△BEA．

解答：解：（1）∵AB⊥AC  CD⊥DE
∴∠BAE+∠CAD=90°，∠CAD+∠DCA=90°，
∴∠DCA=∠EAB；
（2）∵CD⊥DE，BE⊥DE，
∴在△ADC和△BEA中，

∠DCA=∠EAB ∠D=∠E AB=AC

，
∴△ADC≌△BEA．（AAS）

点评：本题考查了全等三角形的判定，熟练运用AAS方法求证三角形全等是解题的关键．