题目内容
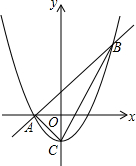 如图,抛物线y=x2-1的顶点为C,直线y=x+1与抛物线交于A,B两点.M是抛物线上一点,过M作MG⊥x轴,垂足为G.如果以A,M,G为顶点的三角形与△ABC相似,那么点M的坐标是
如图,抛物线y=x2-1的顶点为C,直线y=x+1与抛物线交于A,B两点.M是抛物线上一点,过M作MG⊥x轴,垂足为G.如果以A,M,G为顶点的三角形与△ABC相似,那么点M的坐标是考点:二次函数综合题
专题:
分析:根据抛物线的解析式,易求得A(-1,0),D(1,0),C(0,-1);则△ACD是等腰Rt△,由于AP∥DC,可知∠BAC=90°;根据D、C的坐标,用待定系数法可求出直线DC的解析式,而AB∥DC,则直线AB与DC的斜率相同,再加上A点的坐标,即可求出直线AB的解析式,联立直线AB和抛物线的解析式,可求出B点的坐标,即可得出AB、AC的长.在Rt△ABC和Rt△AMG中,已知了∠BAC=∠AGM=90°,若两三角形相似,则直角边对应成比例,据此可求出M点的坐标.
解答: 解:易知:A(-1,0),D(1,0),C(0,-1);
解:易知:A(-1,0),D(1,0),C(0,-1);
则OA=OD=OC=1,
∴△ADC是等腰直角三角形,
∴∠ACD=90°,AC=
;
又∵AB∥DC,
∴∠BAC=90°;
易知直线BD的解析式为y=x-1,
由于直线AB∥DC,可设直线AB的解析式为y=x+b,由于直线AB过点A(-1,0);
则直线AB的解析式为:y=x+1,
联立抛物线的解析式:
,
解得
,
;
故B(2,3);
∴AP=
=3
;
Rt△BAC和Rt△AMG中,∠AGM=∠PAC=90°,且BA:AC=3
:
=3:1;
若以A、M、G三点为顶点的三角形与△BCA相似,则AG:MG=1:3或3:1;
设M点坐标为(m,m2-1),(m<-1或m>1)
则有:MG=m2-1,AG=|m+1|;
①当AM:MG=1:3时,m2-1=3|m+1|,m2-1=±(3m+3);
当m2-1=3m+3时,m2-3m-4=0,解得m=1(舍去),m=4;
当m2-1=-3m-3时,m2+3m+2=0,解得m=-1(舍去),m=-2;
∴M1(4,15),M2(-2,3);
②当AM:MG=3:1时,3(m2-1)=|m+1|,3m2-3=±(m+1);
当3m2-3=m+1时,3m2-m-4=0,解得m=-1(舍去),m=
;
当3m2-3=-m-1时,3m2+m-2=0,解得m=-1(舍去),m=
(舍去);
∴M3(
,
).
故符合条件的M点坐标为:(4,15),(-2,3),(
,
).
故答案为::(4,15),(-2,3),(
,
).
 解:易知:A(-1,0),D(1,0),C(0,-1);
解:易知:A(-1,0),D(1,0),C(0,-1);则OA=OD=OC=1,
∴△ADC是等腰直角三角形,
∴∠ACD=90°,AC=
| 2 |
又∵AB∥DC,
∴∠BAC=90°;
易知直线BD的解析式为y=x-1,
由于直线AB∥DC,可设直线AB的解析式为y=x+b,由于直线AB过点A(-1,0);
则直线AB的解析式为:y=x+1,
联立抛物线的解析式:
|
解得
|
|
故B(2,3);
∴AP=
| (2+1)2+32 |
| 2 |
Rt△BAC和Rt△AMG中,∠AGM=∠PAC=90°,且BA:AC=3
| 2 |
| 2 |
若以A、M、G三点为顶点的三角形与△BCA相似,则AG:MG=1:3或3:1;
设M点坐标为(m,m2-1),(m<-1或m>1)
则有:MG=m2-1,AG=|m+1|;
①当AM:MG=1:3时,m2-1=3|m+1|,m2-1=±(3m+3);
当m2-1=3m+3时,m2-3m-4=0,解得m=1(舍去),m=4;
当m2-1=-3m-3时,m2+3m+2=0,解得m=-1(舍去),m=-2;
∴M1(4,15),M2(-2,3);
②当AM:MG=3:1时,3(m2-1)=|m+1|,3m2-3=±(m+1);
当3m2-3=m+1时,3m2-m-4=0,解得m=-1(舍去),m=
| 4 |
| 3 |
当3m2-3=-m-1时,3m2+m-2=0,解得m=-1(舍去),m=
| 2 |
| 3 |
∴M3(
| 4 |
| 3 |
| 7 |
| 9 |
故符合条件的M点坐标为:(4,15),(-2,3),(
| 4 |
| 3 |
| 7 |
| 9 |
故答案为::(4,15),(-2,3),(
| 4 |
| 3 |
| 7 |
| 9 |
点评:此题主要考查了函数图象交点、直角三角形的判定、相似三角形的判定和性质等,需注意的是在相似三角形的对应边和对应角不确定的情况下需分类讨论,以免漏解.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
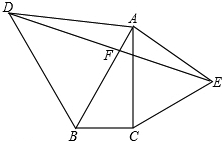 如图,在△ABC中,∠ABC=60°,分别以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接DE,交AB于点F,求证:DF=EF.
如图,在△ABC中,∠ABC=60°,分别以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接DE,交AB于点F,求证:DF=EF.
 如图,已知AB=AE,BC=ED,AC=AD.
如图,已知AB=AE,BC=ED,AC=AD.