题目内容
14.先化简,再求值:$\frac{{x}^{2}}{{x}^{2}-1}$÷(1+$\frac{1}{x-1}$),其中x=$\sqrt{2}-1$.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{{x}^{2}}{(x+1)(x-1)}$÷$\frac{x}{x-1}$=$\frac{{x}^{2}}{(x+1)(x-1)}$•$\frac{x-1}{x}$=$\frac{x}{x+1}$,
当x=$\sqrt{2}$-1时,原式=$\frac{\sqrt{2}-1}{\sqrt{2}-1+1}$=1-$\frac{\sqrt{2}}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知点A的坐标是(a,b),若a+b<0,ab>0,则它在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
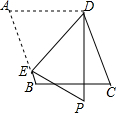 如图,在平行四边形ABCD中,点E为AB边上一点,将△AED沿直线DE翻折,点A落在点P处,且DP⊥BC,则∠EDP=45°.
如图,在平行四边形ABCD中,点E为AB边上一点,将△AED沿直线DE翻折,点A落在点P处,且DP⊥BC,则∠EDP=45°.