题目内容
19.从-3、-1、$\frac{1}{2}$、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为$\frac{3}{5}$.分析 直接分别带入各数求出三角形面积进而得出答案.
解答 解:当a=-3,则y=-x-3,此时图象与x轴交点为:(-3,0),与y轴交点为:(0,-3),
故一次函数y=-x+a的图象与坐标轴围成三角形的面积为4.5,不合题意;
当a=3,则y=-x+3,此时图象与x轴交点为:(3,0),与y轴交点为:(0,3),
故一次函数y=-x+a的图象与坐标轴围成三角形的面积为4.5,不合题意;
当a=-1、$\frac{1}{2}$、1时,一次函数y=-x+a的图象与坐标轴围成三角形的面积为:$\frac{1}{2}$,$\frac{1}{4}$,符合题意,
故关于x的一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为:$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 此题考查了概率公式的应用以及一次函数图象上点的坐标特征.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.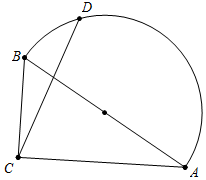 如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
 如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )| A. | π或$\frac{π}{2}$ | B. | $\frac{π}{2}$或$\frac{π}{3}$ | C. | $\frac{π}{3}$或π | D. | $\frac{π}{4}$或$\frac{π}{3}$ |