题目内容
20.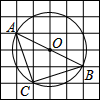 如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作△ABC的外接圆⊙O,则弧AC的长等于( )
如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作△ABC的外接圆⊙O,则弧AC的长等于( )| A. | π | B. | $\frac{\sqrt{10}π}{2}$ | C. | $\frac{\sqrt{5}π}{4}$ | D. | $\frac{\sqrt{5}π}{2}$ |
分析 根据勾股定理可计算出AB2、AC2、BC2,从而得到AB2=AC2+BC2,CA=CB,根据勾股定理的逆定理可得∠ACB=90°,再根据圆周角定理可得AB是⊙O的直径,根据CA=CB,可得弧AC的长等于弧BC的长,只需求出弧AB的长,就可解决问题.
解答 解:根据勾股定理可得:
AB2=42+22=20,AC2=32+12=10,BC2=32+12=10,
∴AB2=AC2+BC2,CA=CB,
∴∠ACB=90°,
∴AB是⊙O的直径,
∴弧AB的长=$\frac{1}{2}$×π×AB=$\frac{1}{2}$×π×2$\sqrt{5}$=$\sqrt{5}$π,
∵CA=CB,
∴弧AC的长=弧BC的长=$\frac{1}{2}$×弧AB的长=$\frac{\sqrt{5}π}{2}$.
故选D.
点评 本题以网格为背景,主要考查了弧长的计算,勾股定理及其逆定理、圆周角定理、同圆中弧与弦的关系等知识,难度不大,但考查的知识面广,是一道好题.

练习册系列答案
相关题目
10.若4x2-9=0,则x的值是( )
| A. | ±$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{3}{2}$ | D. | $\frac{9}{4}$ |
15. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=25°,则∠2的度数为( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=25°,则∠2的度数为( )
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=25°,则∠2的度数为( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=25°,则∠2的度数为( )| A. | 10° | B. | 20° | C. | 25° | D. | 35° |
12.数据10,10,x,8的众数与平均数相同,那么x的值是( )
| A. | 10 | B. | 8 | C. | 12 | D. | 4 |
9. 如图,数轴上A、B两点分别对应实数a、b,则下列结论中正确的是( )
如图,数轴上A、B两点分别对应实数a、b,则下列结论中正确的是( )
 如图,数轴上A、B两点分别对应实数a、b,则下列结论中正确的是( )
如图,数轴上A、B两点分别对应实数a、b,则下列结论中正确的是( )| A. | a+b>0 | B. | ab>0 | C. | $\frac{|a|}{a}$+$\frac{|b|}{b}$=0 | D. | a+ab-b<0 |
10.已知正比例函数y=(m-1)x,若y的值随x的增大而增大,则点(m,1-m)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 各顶点都在格点上的三角形叫格点三角形,如图,在4×8的方格中,以M、N为顶点且与△ABC相似的格点三角形的个数共有( )个.
各顶点都在格点上的三角形叫格点三角形,如图,在4×8的方格中,以M、N为顶点且与△ABC相似的格点三角形的个数共有( )个.