题目内容
16. 把长方形按如图所示折叠,已知CD=8,DE=5,求AE的长.
把长方形按如图所示折叠,已知CD=8,DE=5,求AE的长.
分析 先根据长方形对边相等得AB=8,由折叠得:∠BDC=∠BDC′,因为AB∥CD得内错角相等,所以△BED是等腰三角形,得BE=DE=5,则AE=3.
解答 解:∵四边形ABCD为长方形,
∴AB=CD=8,AB∥CD,
∴∠ABD=∠BDC,
由折叠得:∠BDC=∠BDC′,
∴BE=DE=5,
∴AE=AB-BE=8-5=3.
点评 本题是折叠问题,考查了折叠和长方形的性质,知道长方形的对边相等且平行;熟知折叠前后的边相等、角相等;与等腰三角形中等角对等边结合,得出结论.

练习册系列答案
相关题目
7.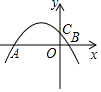 如图,抛物线y=-x2+bx+c的图象与x轴交于A、B两点,与y轴相交于点C,如果OB=OC=$\frac{1}{2}$OA,那么b的值为( )
如图,抛物线y=-x2+bx+c的图象与x轴交于A、B两点,与y轴相交于点C,如果OB=OC=$\frac{1}{2}$OA,那么b的值为( )
 如图,抛物线y=-x2+bx+c的图象与x轴交于A、B两点,与y轴相交于点C,如果OB=OC=$\frac{1}{2}$OA,那么b的值为( )
如图,抛物线y=-x2+bx+c的图象与x轴交于A、B两点,与y轴相交于点C,如果OB=OC=$\frac{1}{2}$OA,那么b的值为( )| A. | -2 | B. | -1 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
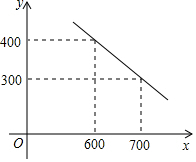 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,也不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似于一次函数y=kx+b的关系,如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,也不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似于一次函数y=kx+b的关系,如图所示.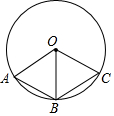 如图,OA,OB,OC是⊙O的三条半径.
如图,OA,OB,OC是⊙O的三条半径. 已知:如图,在△ABC中,AB=AC,点D,E,F分别在边BC,BA,CA上,且BE=CD,BD=CF.求证:点D在线段EF的垂直平分线上.
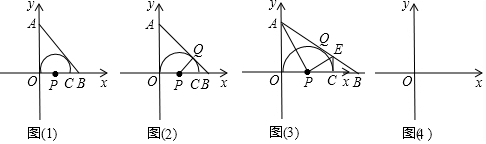
已知:如图,在△ABC中,AB=AC,点D,E,F分别在边BC,BA,CA上,且BE=CD,BD=CF.求证:点D在线段EF的垂直平分线上.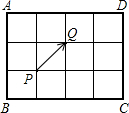 如图是一个小型的台球桌,四角分别是A,B,C,D四个球筐,桌面可以分成12个正方形小区域,如果将在点P位置的球沿着PQ的方向击球Q,那么球Q最终会落在( )
如图是一个小型的台球桌,四角分别是A,B,C,D四个球筐,桌面可以分成12个正方形小区域,如果将在点P位置的球沿着PQ的方向击球Q,那么球Q最终会落在( )