题目内容
4.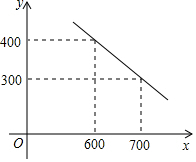 某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,也不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似于一次函数y=kx+b的关系,如图所示.
某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,也不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似于一次函数y=kx+b的关系,如图所示.(1)根据图象,求一次函数y=kx+b的表达式;
(2)设公司获得的毛利润为S元,试问销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时销售量是多少?
分析 (1)根据函数图象上的点可以求得一次函数y=kx+b的表达式;
(2)根据(1)中的函数解析式和S=(x-500)y,可以解答本题.
解答 解:(1)∵点(600,400),(700,300)在y=kx+b上,
∴$\left\{\begin{array}{l}{600k+b=400}\\{700k+b=300}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-1}\\{b=1000}\end{array}\right.$
即一次函数的表达式是y=-x+1000(500≤x≤800);
(2)S=(-x+1000)(x-500)=-x2+1500x-500000=-(x-750)2+62500,
∴x=750时,S取得最大值,此时S=62500,y=-750+1000=250,
即销售单价定为750元时,该公司获得最大毛利润,最大毛利润是62500元,此时销售量是250件.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,列出相应的函数解析式,会求函数的最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.某股民在上周星期五买进某种股票500股,每股60元,下表是本周股票的涨跌情况(单位:元):
(1)本周星期五收盘时,每股是多少元?
(2)已知买进股票时付了0.15%的手续费,卖出股票时需付成交额0.15%的手续费和0.1%的交易费,若在本周五收盘前将全部股票一次性地卖出,他的收益如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +2 | -0.5 | +1.5 | -1.8 | +0.8 |
(2)已知买进股票时付了0.15%的手续费,卖出股票时需付成交额0.15%的手续费和0.1%的交易费,若在本周五收盘前将全部股票一次性地卖出,他的收益如何?
12.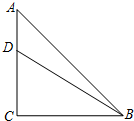 如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
 如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
19.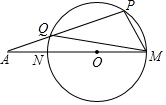 如图,MN是⊙O的直径,∠A=20°,∠PMQ=50°,以PM为边作圆的内接正多边形,则这个正多边形是( )
如图,MN是⊙O的直径,∠A=20°,∠PMQ=50°,以PM为边作圆的内接正多边形,则这个正多边形是( )
 如图,MN是⊙O的直径,∠A=20°,∠PMQ=50°,以PM为边作圆的内接正多边形,则这个正多边形是( )
如图,MN是⊙O的直径,∠A=20°,∠PMQ=50°,以PM为边作圆的内接正多边形,则这个正多边形是( )| A. | 正七边形 | B. | 正八边形 | C. | 正六边形 | D. | 正十边形 |
 如图,在由边长为1的小正方形组成的10×10的网格中(组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.
如图,在由边长为1的小正方形组成的10×10的网格中(组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上. 把长方形按如图所示折叠,已知CD=8,DE=5,求AE的长.
把长方形按如图所示折叠,已知CD=8,DE=5,求AE的长. 将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
将连续的奇数1,3,5,7,9,…,排成如图所示的数阵. 如图,已知BE⊥AD,CF⊥AD,且BE=CF.
如图,已知BE⊥AD,CF⊥AD,且BE=CF.