题目内容
16.若关于x的不等式组$\left\{\begin{array}{l}{x+6<2+3x}\\{\frac{a+2x}{4}>x}\end{array}\right.$有且只有四个整数解,则实数a的取值范围是12<a≤14.分析 此题可先根据一元一次不等式组解出x的取值,再根据不等式组只有四个整数解,求出实数a的取值范围.
解答 解:$\left\{\begin{array}{l}{x+6<2+3x①}\\{\frac{a+2x}{4}>x②}\end{array}\right.$
解①得x>2,
解②得x<$\frac{1}{2}$a,
∴2<x$<\frac{1}{2}a$,
∵不等式组$\left\{\begin{array}{l}{x+6<2+3x}\\{\frac{a+2x}{4}>x}\end{array}\right.$有且只有四个整数解,即3,4,5,6;
∴6<$\frac{1}{2}$a≤7,即12<a≤14.
故答案为12<a≤14.
点评 此题考查的是一元一次不等式的解法和一元一次方程的解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了

练习册系列答案
相关题目
11.下列各数中,最小的数是( )
| A. | 5 | B. | -$\sqrt{3}$ | C. | π | D. | -1 |
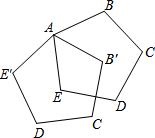 如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=54°.
如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=54°.