题目内容
17.把下列各数填入相应的大括号内.$\sqrt{3}$,-2,$\root{3}{9}$,0,$\root{3}{-8}$,$\frac{16}{113}$,3.1415,π-3,$\sqrt{144}$,3+$\sqrt{29}$,3$\sqrt{2}$,0.2121121112…整数集合:{ …};
非负实数集合:{ …};
无理数集合:{ …}.
分析 (1)整数:像-2,-1,0,1,2…这样的数称为整数,整数分为正整数、负整数和0,据此找出整数有哪些即可;
(2)非负实数包括正实数和0,据此判断即可;
(3)有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数,据此判断出无理数有哪些即可.
解答 解:整数集合:{-2,0,$\root{3}{-8}$,$\sqrt{144}$,…};
非负实数集合:{$\sqrt{3}$,$\root{3}{9}$,0,$\frac{16}{113}$,3.1415,π-3,$\sqrt{144}$,3+$\sqrt{29}$,3$\sqrt{2}$,0.2121121112…,…};
无理数集合:{$\sqrt{3}$,$\root{3}{9}$,π-3,3+$\sqrt{29}$,3$\sqrt{2}$,0.2121121112…,…}.
故答案为:-2,0,$\root{3}{-8}$,$\sqrt{144}$;
$\sqrt{3}$,$\root{3}{9}$,0,$\frac{16}{113}$,3.1415,π-3,$\sqrt{144}$,3+$\sqrt{29}$,3$\sqrt{2}$,0.2121121112…;
$\sqrt{3}$,$\root{3}{9}$,π-3,3+$\sqrt{29}$,3$\sqrt{2}$,0.2121121112….
点评 此题主要考查了实数的分类,要熟练掌握,解答此题的关键是要明确实数的定义:有理数和无理数统称实数.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
12.正六边形的边长等于2,则这个正六边形的面积等于( )
| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 7$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
7.计算[-2(-xn-1)]3=( )
| A. | -2x3n-1 | B. | 8x3n-3 | C. | 16x3n-3 | D. | -16x3n-3 |
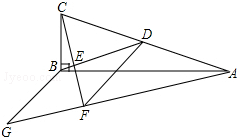 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若FG=5,CF=6,则四边形BDFG的面积为15.
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若FG=5,CF=6,则四边形BDFG的面积为15.
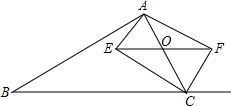 如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F