题目内容
20. 某校了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:
某校了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成不完整的统计图表:| 阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
(1)分别求出统计表中的x、y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.
分析 (1)首先求得总分数,然后即可求得x和y的值;
(2)首先求得样本中的优秀率,然后用样本估计总体即可;
(3)列表将所有等可能的结果列举出来,然后利用概率公式求解即可.
解答 解:(1)由表可知被调查学生中“一般”档次的有13人,所占比例是26%,所以共调查的学生数是13÷26%=50,
则调查学生中“良好”档次的人数为50×60%=30,
∴x=30-(12+7)=11,
y=50-(1+2+6+7+12+11+7+1)=3.
(2)由样本数据可知“优秀”档次所占的百分比为$\frac{3+1}{50}$=8%,
∴,估计九年级400名学生中为优秀档次的人数为400×8%=32;
(3)用A、B、C表示阅读本数是8的学生,用D表示阅读9本的学生,列表得到:
| A | B | C | D | |
| A | AB | AC | AD | |
| B | BA | BC | BD | |
| C | CA | CB | CD | |
| D | DA | DB | DC |
所以抽取的2名学生中有1名阅读本数为9的概率为$\frac{6}{12}$=$\frac{1}{2}$;
点评 考查了列表与树状图法求概率、用样本估计总体及扇形统计图的知识,解题的关键是能够通过列表将所有等可能的结果列举出来,难度不大.

练习册系列答案
相关题目
8.如图汽车标志中不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5. 如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
 如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )| A. | ∠ABC=90° | B. | AC=BD | C. | OA=OB | D. | OA=AD |
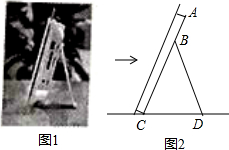 如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为14.1cm(参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm,可用科学计算器).
如图1是小志同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=15cm,∠CBD=40°,则点B到CD的距离为14.1cm(参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm,可用科学计算器).