题目内容
10．
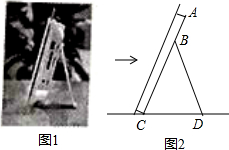如图1是小志同学书桌上的一个电子相框，将其侧面抽象为如图2所示的几何图形，已知BC=BD=15cm，∠CBD=40°，则点B到CD的距离为14.1cm（参考数据sin20°≈0.342，cos20°≈0.940，sin40°≈0.643，cos40°≈0.766，结果精确到0.1cm，可用科学计算器）．
分析 作BE⊥CD于E，根据等腰三角形的性质和∠CBD=40°，求出∠CBE的度数，根据余弦的定义求出BE的长．
解答 
解：如图2，作BE⊥CD于E，
∵BC=BD，∠CBD=40°，
∴∠CBE=20°，
在Rt△CBE中，cos∠CBE=$\frac{BE}{BC}$，
∴BE=BC•cos∠CBE
=15×0.940
=14.1cm．
故答案为：14.1．
点评 本题考查的是解直角三角形的应用，掌握锐角三角函数的概念是解题的关键，作出合适的辅助线构造直角三角形是解题的重要环节．
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
如图，几何体上半部为正三棱柱，下半部为圆柱，其俯视图是（ ）
19．
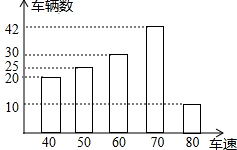为了了解一路段车辆行驶速度的情况，交警统计了该路段上午7：：0至9：00来往车辆的车速（单位：千米/时），并绘制成如图所示的条形统计图．这些车速的众数、中位数分别是（ ）
为了了解一路段车辆行驶速度的情况，交警统计了该路段上午7：：0至9：00来往车辆的车速（单位：千米/时），并绘制成如图所示的条形统计图．这些车速的众数、中位数分别是（ ）| A． | 众数是80千米/时，中位数是60千米/时 | |
| B． | 众数是70千米/时，中位数是70千米/时 | |
| C． | 众数是60千米/时，中位数是60千米/时 | |
| D． | 众数是70千米/时，中位数是60千米/时 |
20．
某校了解九年级学生近两个月“推荐书目”的阅读情况，随机抽取了该年级的部分学生，调查了他们每人“推荐书目”的阅读本数．设每名学生的阅读本数为n，并按以下规定分为四档：当n＜3时，为“偏少”；当3≤n＜5时，为“一般”；当5≤n＜8时，为“良好”；当n≥8时，为“优秀”．将调查结果统计后绘制成不完整的统计图表：
请根据以上信息回答下列问题：
（1）分别求出统计表中的x、y的值；
（2）估计该校九年级400名学生中为“优秀”档次的人数；
（3）从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会，请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率．
某校了解九年级学生近两个月“推荐书目”的阅读情况，随机抽取了该年级的部分学生，调查了他们每人“推荐书目”的阅读本数．设每名学生的阅读本数为n，并按以下规定分为四档：当n＜3时，为“偏少”；当3≤n＜5时，为“一般”；当5≤n＜8时，为“良好”；当n≥8时，为“优秀”．将调查结果统计后绘制成不完整的统计图表：| 阅读本数n（本） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 人数（名） | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
（1）分别求出统计表中的x、y的值；
（2）估计该校九年级400名学生中为“优秀”档次的人数；
（3）从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会，请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率．