题目内容
 如图,已知△ABE≌△ACD,求证:∠1=∠2.
如图,已知△ABE≌△ACD,求证:∠1=∠2.考点:全等三角形的性质
专题:证明题
分析:由△ABE≌△ACD,根据全等三角形的对应角(边)相等,可得AD=AE,∠ADC=∠AEB,然后根据等边对等角可得∠ADE=∠AED,最后根据等式的性质可得:∠1=∠2.
解答:证明:∵△ABE≌△ACD,
∴AD=AE,∠ADC=∠AEB,
∴∠ADE=∠AED,
∴∠ADC-∠ADE=∠AEB-∠AED,
即:∠1=∠2.
∴AD=AE,∠ADC=∠AEB,
∴∠ADE=∠AED,
∴∠ADC-∠ADE=∠AEB-∠AED,
即:∠1=∠2.
点评:此题考查了全等三角形的性质,熟记全等三角形的对应角(边)相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A、3cm | B、6cm |
| C、9cm | D、12cm |

 如图,已知AD∥BC,∠1=∠2,说明∠3与∠4有什么关系,并说明理由.
如图,已知AD∥BC,∠1=∠2,说明∠3与∠4有什么关系,并说明理由. CD是⊙O的直径,AB是弦,且AB⊥CD,垂足是E,如果CE=2、AB=8,那么ED=
CD是⊙O的直径,AB是弦,且AB⊥CD,垂足是E,如果CE=2、AB=8,那么ED=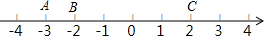 如图所示,在数轴上有三个点,A,B,C,回答下列问题.
如图所示,在数轴上有三个点,A,B,C,回答下列问题. 如图,?ABCD中,E是BC的中点,AE=9,BD=12,AD=10.
如图,?ABCD中,E是BC的中点,AE=9,BD=12,AD=10. 如图,每个面上都有一个汉字的正方体的一种展开图,那么在原正方体“着”相对的面上的汉字是
如图,每个面上都有一个汉字的正方体的一种展开图,那么在原正方体“着”相对的面上的汉字是 如图所示,直线a,b被直线c所截,a∥b,∠1=110°,∠2=
如图所示,直线a,b被直线c所截,a∥b,∠1=110°,∠2=