题目内容
15. 如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=11,AC=5,则BE=3.
如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=11,AC=5,则BE=3.
分析 连接CD,BD,由∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,根据角平分线的性质与线段垂直平分线的性质,易得CD=BD,DF=DE,继而可得AF=AE,易证得Rt△CDF≌Rt△BDE,则可得BE=CF,继而求得答案.
解答 解:如图,连接CD,BD,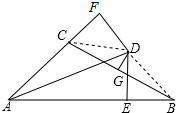
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,
∴AE=AF,
∵DG是BC的垂直平分线,
∴CD=BD,
在Rt△CDF和Rt△BDE中,$\left\{\begin{array}{l}{CD=BD}\\{DF=DE}\end{array}\right.$,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,
∵AB=11,AC=5,
∴BE=$\frac{1}{2}$(11-5)=3.
故答案为:3.
点评 此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
3.“任意买一张电影票,座位号是奇数”,此事件是( )
| A. | 不可能事件 | B. | 不确定事件 | C. | 必然事件 | D. | 确定事件 |
10.化简$\frac{x-2}{x+2}+\frac{x+2}{2-x}$的结果是( )
| A. | $\frac{-8x}{{x}^{2}-4}$ | B. | $\frac{-8x}{{x}^{2}+4}$ | C. | $\frac{8x}{{x}^{2}-4}$ | D. | $\frac{2{x}^{2}+8}{{x}^{2}-4}$ |
20.若△ABC的边长分别为a,b,c,则不能确定此三角形是直角三角形的是( )
| A. | a+b+c=12 | B. | ∠A+∠B=∠C | C. | ∠A:∠B:∠C=1:2:3 | D. | a2+b2=c2 |
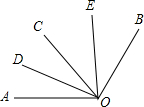 如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.
如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.