题目内容
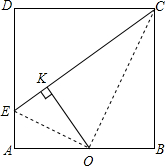 如图,在正方形ABCD的一边上取一点E,使AE=
如图,在正方形ABCD的一边上取一点E,使AE=| 1 |
| 4 |
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:如图,证明AE:BO=AO:BC,结合∠A=∠B,得到△AOE∽△BCO;进而证明∠EOC=90°,运用射影定理即可解决问题.
解答: 解:OK2=EK•KC成立;理由如下:
解:OK2=EK•KC成立;理由如下:
∵四边形ABCD是正方形,
∴∠A=∠B=90°,AB=AD=BC(设为λ);
在△AOE与△BCO中,
∵AE:OB=
λ:
λ=1:2,AO:BC=
λ:λ=1:2,
∴AE:BO=AO:BC,而∠A=∠B,
∴△AOE∽△BCO,
∴∠AOE=∠BCO;而∠BOC+∠BCO=90°,
∴∠AOE+∠BOC=90°,
∴∠EOC=180°-90°=90°;
∵OK⊥EC,
∴OK2=EK•KC(射影定理).
 解:OK2=EK•KC成立;理由如下:
解:OK2=EK•KC成立;理由如下:∵四边形ABCD是正方形,
∴∠A=∠B=90°,AB=AD=BC(设为λ);
在△AOE与△BCO中,
∵AE:OB=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AE:BO=AO:BC,而∠A=∠B,
∴△AOE∽△BCO,
∴∠AOE=∠BCO;而∠BOC+∠BCO=90°,
∴∠AOE+∠BOC=90°,
∴∠EOC=180°-90°=90°;
∵OK⊥EC,
∴OK2=EK•KC(射影定理).
点评:该题以正方形为载体,主要考查了正方形的性质、相似三角形的判定及其性质、射影定理等几何知识点的应用问题;解题的关键是灵活运用正方形的性质等知识点来证明△AOE∽△BCO,进而证明证明△COE为直角三角形.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
近些年,中国城市中产阶级规模快速扩大,2012年增至413 000 000人,用科学记数法表示为( )人.
| A、413×106 |
| B、4.13×108 |
| C、4.13×106 |
| D、0.413×109 |
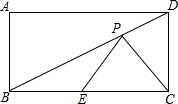 如图,若ABCD是矩形,AB=10cm,BC=20cm,E为边BC上的一个动点,P为BD上的一个动点,求PC+PE的最小值.
如图,若ABCD是矩形,AB=10cm,BC=20cm,E为边BC上的一个动点,P为BD上的一个动点,求PC+PE的最小值.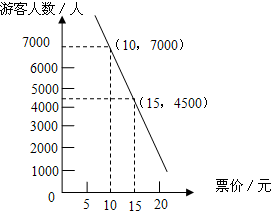 某游乐场采取了浮动门票价格的方法来控制游客人数.在该方法实施过程中发现:每周游客人数与票价之间存在着如图所示的一次函数关系.在这样的情况下,如果限定票价在5~20元间浮动,那么每周游客人数最多可能是多少?
某游乐场采取了浮动门票价格的方法来控制游客人数.在该方法实施过程中发现:每周游客人数与票价之间存在着如图所示的一次函数关系.在这样的情况下,如果限定票价在5~20元间浮动,那么每周游客人数最多可能是多少?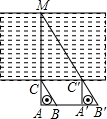 如图,一名同学拿一把含30°角直角三角尺ABC(即∠ACB=30°)目测一条河的宽度,他先在岸边点A处顺着30°角的邻边AC的方向看见河对岸的一棵树M,然后沿30°角的对边AB的方向前进到B′处,顺着斜边B′C′的方向看见树M,并测得AA′=100米,则他目测的河宽MC大约是多少米(精确到1米)?
如图,一名同学拿一把含30°角直角三角尺ABC(即∠ACB=30°)目测一条河的宽度,他先在岸边点A处顺着30°角的邻边AC的方向看见河对岸的一棵树M,然后沿30°角的对边AB的方向前进到B′处,顺着斜边B′C′的方向看见树M,并测得AA′=100米,则他目测的河宽MC大约是多少米(精确到1米)? 如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB-BC的理由.
如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB-BC的理由.