题目内容
如图,等腰直角△BCD,∠BDC=90°,E为CD的中点,DF⊥BE于F,连CF交BD于H.
(1)求证:DE2=EF•EB;
(2)求
;
(3)过B点作BG⊥BC交CH的延长线于G点,求证:BC=2BG.
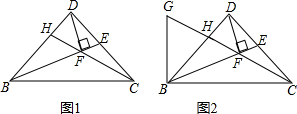
(1)求证:DE2=EF•EB;
(2)求
| DH |
| BH |
(3)过B点作BG⊥BC交CH的延长线于G点,求证:BC=2BG.

考点:相似三角形的判定与性质
专题:
分析:(1)利用条件可证明△DEF∽△BED,再利用相似三角形的性质可证得结论;
(2)可证明△BFD∽△DFE,可得到BF和EF的关系,过E作EM∥BD交CH于M,可找到DH和EM的关系,BH和EM的关系,从而可求得
;
(3)过D作DN⊥BC,交CH于L,交BC于点N,可证得DL=LN=
BG,可得BG=DN,可证得BC=2BG.
(2)可证明△BFD∽△DFE,可得到BF和EF的关系,过E作EM∥BD交CH于M,可找到DH和EM的关系,BH和EM的关系,从而可求得
| DH |
| BH |
(3)过D作DN⊥BC,交CH于L,交BC于点N,可证得DL=LN=
| 1 |
| 2 |
解答:(1)证明:
∵DF⊥BE,
∴∠DFE=∠BDE=90°,且∠DEF=∠BED,
∴△DEF∽△BED,
∴
=
,
∴DE2=EF•EB;
(2)解:
∵DF⊥BE,
∴∠DFB=∠DFE=90°,
∴∠DBF+∠BDF=∠BDF+∠FDE=90°,
∴∠DBF=∠FDE,
∴△BFD∽△DFE,
∴
=
=
,
∵BD=CD,E为CD中点,
∴
=2,
∴BF=2DF=4EF,
如图1,过点E作EM∥BD,交CH于点M,
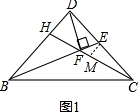
∵E为CD中点,
∴M为CH中点,
∴DH=2FM,
∵FM∥BD,
∴
=
=4,
∴BH=4FM,
∴
=
=
;
(3)证明:
如图2,过D作DN⊥BC,交CG于点L,交BC于点N,
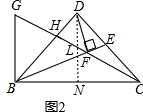
∵GB⊥BC,
∴DN∥BG,
∵△BCD为等腰直角三角形,
∴BN=CN=DN,
∴L为CG中点,
∴GB=2LN,
∵GB∥DL,
∴
=
=2,
∴GB=2DL,
∴GB=DN=
BC,
∴BC=2GB.
∵DF⊥BE,
∴∠DFE=∠BDE=90°,且∠DEF=∠BED,
∴△DEF∽△BED,
∴
| DE |
| BE |
| EF |
| DE |
∴DE2=EF•EB;
(2)解:
∵DF⊥BE,
∴∠DFB=∠DFE=90°,
∴∠DBF+∠BDF=∠BDF+∠FDE=90°,
∴∠DBF=∠FDE,
∴△BFD∽△DFE,
∴
| BF |
| DF |
| DF |
| EF |
| BD |
| DE |
∵BD=CD,E为CD中点,
∴
| BD |
| DE |
∴BF=2DF=4EF,
如图1,过点E作EM∥BD,交CH于点M,

∵E为CD中点,
∴M为CH中点,
∴DH=2FM,
∵FM∥BD,
∴
| BH |
| FM |
| BF |
| EF |
∴BH=4FM,
∴
| DH |
| BH |
| 2FM |
| 4FM |
| 1 |
| 2 |
(3)证明:
如图2,过D作DN⊥BC,交CG于点L,交BC于点N,

∵GB⊥BC,
∴DN∥BG,
∵△BCD为等腰直角三角形,
∴BN=CN=DN,
∴L为CG中点,
∴GB=2LN,
∵GB∥DL,
∴
| GB |
| DL |
| BH |
| DH |
∴GB=2DL,
∴GB=DN=
| 1 |
| 2 |
∴BC=2GB.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的对应边成比例是解题的关键,注意利用中点构造三角形中位线是解题的常用辅助线.

练习册系列答案
相关题目
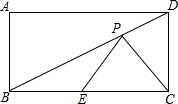 如图,若ABCD是矩形,AB=10cm,BC=20cm,E为边BC上的一个动点,P为BD上的一个动点,求PC+PE的最小值.
如图,若ABCD是矩形,AB=10cm,BC=20cm,E为边BC上的一个动点,P为BD上的一个动点,求PC+PE的最小值.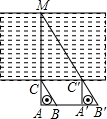 如图,一名同学拿一把含30°角直角三角尺ABC(即∠ACB=30°)目测一条河的宽度,他先在岸边点A处顺着30°角的邻边AC的方向看见河对岸的一棵树M,然后沿30°角的对边AB的方向前进到B′处,顺着斜边B′C′的方向看见树M,并测得AA′=100米,则他目测的河宽MC大约是多少米(精确到1米)?
如图,一名同学拿一把含30°角直角三角尺ABC(即∠ACB=30°)目测一条河的宽度,他先在岸边点A处顺着30°角的邻边AC的方向看见河对岸的一棵树M,然后沿30°角的对边AB的方向前进到B′处,顺着斜边B′C′的方向看见树M,并测得AA′=100米,则他目测的河宽MC大约是多少米(精确到1米)?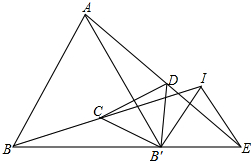 如图,已知△ABB′与△IB′E是等边三角形,连接AE、BI,C、D分别为BI、AE的中点,求证:△CDB′是等边三角形.
如图,已知△ABB′与△IB′E是等边三角形,连接AE、BI,C、D分别为BI、AE的中点,求证:△CDB′是等边三角形.