题目内容
14. 阅读下面的材料:
阅读下面的材料:1750年,欧拉在写给哥德巴赫的信中列举了多面体的一些性质,其中一条是:如果用V、E、F分别表示凸多面体的顶点数、棱数、面数,则有V-E+F=2.这个发现,就是著名的欧拉定理.
根据所阅读的材料,完成:
据百度百科介绍:C60是一种由60个碳原子构成的分子,这种分子的微观结构是个多面体,形似足球,故名足球烯.C60具有金属光泽,有许多优异性能,如超导、强磁性、耐高压、抗化学腐蚀等,在光、电、磁等领域有潜在的应用前景.已知足球烯的分子具有60个顶点和32个面,其中12个为正五边形,20个为正六边形.那么,这种多面体的棱数是90.
分析 根据V、E、F分别表示凸多面体的顶点数、棱数、面数,则有V-E+F=2,直接代入即可求得.
解答 解:根据欧拉定理得,60-E+32=2,
解得E=90.
故答案为90.
点评 本题考查了欧拉定理的应用,熟练掌握欧拉定理是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
4.下列语句叙述正确的个数是( )
①横坐标与纵坐标互为相反数的点在直线y=-x上;
②点P(2,0)在y轴上;
③若点P的坐标为(a,b),且ab=0,则P点是坐标原点;
④函数y=1-x中y随x的增大而增大.
①横坐标与纵坐标互为相反数的点在直线y=-x上;
②点P(2,0)在y轴上;
③若点P的坐标为(a,b),且ab=0,则P点是坐标原点;
④函数y=1-x中y随x的增大而增大.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19. 如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
 如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
6.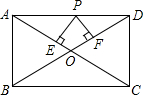 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为( )
如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为( )
 如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为( )
如图,在矩形ABCD中,AB=3,AD=4,P是AD上不与A、D重合的一动点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF的值为( )| A. | 2 | B. | 2.4 | C. | 2.5 | D. | 2.6 |
3.△ABC中,BC=AC,D是AB上一点,连结CD,且AD=BD=CD,则∠A的度数为( )
| A. | 45° | B. | 36° | C. | 90° | D. | 135° |
4.二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
由表可知当x>2时,y随x的增大而增大;当y<5时,x的取值范围是0<x<4.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
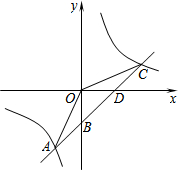 如图,一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数$y=\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.